- 主要内容
- 一些贪心的题:区间问题、Huffman树、排列不等式、其他类型
区间问题
区间问题的贪心一般都是上来先按左端点or右端点排序
然后手动模拟一下贪心,找性质,多找几组样例试试
AcWing905 区间选点
题意
给定N个闭区间,在数轴上选择尽量少的点,使每个区间至少包含一个选出的点,求选择的点的最小数量
思路

- 将每个区间按右端点从小到大排序
- 按照这个顺序从小到大枚举每个区间
- 对于当前区间,比如首先选择区间①的右端点,区间②、③都包含该点,所以直接pass(不在②、③区间选择点),继续往后枚举
- 当枚举到区间④时,发现区间①的右端点不在区间④内,所以此时选择区间④的右端点
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| #include<bits/stdc++.h>
using namespace std;
const int N = 100010,INF=2e9;
int n,ans;
struct Range{
int l,r;
bool operator< (const Range&W)const{
return r<W.r;
}
}range[N];
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=0;i<n;i++) cin>>range[i].l>>range[i].r;
sort(range,range+n);
int ed=-INF;
for(int i=0;i<n;i++){
if(ed<range[i].l){
ans++;
ed=range[i].r;
}
}
cout<<res<<endl;
return 0 ;
}
|
AcWing908 最大不相交区间数量
题意
给定N个闭区间,在数轴上选择若干区间,之间互不相交,求可选区间的最大数量
思路
- 实际上和上题一样,区间相交 == 这几个区间能被同一个点覆盖 == 就只能从这几个区间中选择一个区间
代码
AcWing906 区间分组
优先队列
简单的理解,就是一种可以自动排序的队列
1
2
3
4
5
6
7
8
9
10
| #include<queue>
priority_queue<结构名,vector<结构名>,greater/less<结构名>> 队列名
priority_queue<int,vector<int>,greater<int>>heap;
heap.size();
heap.empty();
heap.push(k);
heap.pop();
heap.top();
|
题意
给定N个闭区间,将其分组,使得每组里面的各个区间没有交集,求最小分组数量
思路
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include<bits/stdc++.h>
#include<queue>
using namespace std;
const int N=1e5+10;
int n;
struct Range{
int l,r;
bool operator<(const Range&M)const{
return l<M.l;
}
}range[N];
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=0;i<n;i++){
int l,r;
cin>>range[i].l>>range[i].r;
}
sort(range,range+n);
priority_queue<int,vector<int>,greater<int>> heap;
for(int i=0;i<n;i++){
if(heap.empty()||heap.top()>=range[i].l){
heap.push(range[i].r);
}else{
heap.pop();
heap.push(range[i].r);
}
}
cout<<heap.size()<<endl;
return 0;
}
|
AcWing907 区间覆盖
题意
N个闭区间,一个线段区间[s,t] ,选择尽量少的区间,将指定线段区间完全覆盖
思路
- 将所有区间按左端点从小到大排序
- 从前往后依次枚举每个区间,
- 在所有能覆盖s(左端点≤s的情况下)的区间中,选择一个右端点最大的区间
- 然后,将s更新为右端点的最大值
- 直到右端点大于t
代码
Huffman树
AcWing148 合并果子
题意
N堆果子,每次任意合并两堆,每次合并消耗的体积等于这两堆重量之和,求合并完消耗的最小体力
思路
经典huffman模型,每次合并重量最小的两堆
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #include<bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);
int n,ans=0;
cin>>n;
priority_queue<int,vector<int>,greater<int> >heap;
for(int i=0;i<n;i++){
int a;cin>>a;
heap.push(a);
}
while(heap.size()>1){
int a=heap.top();heap.pop();
int b=heap.top();heap.pop();
ans+=(a+b);
heap.push(a+b);
}
cout<<ans<<endl;
}
|
排序不等式
AcWing913 排队打水
题意
n个人排队打水,第i个人装满水的时间是ti,问如何排队使得所有人等待时间之和最小
思路

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e5+10;
ll a[N];
ll n,ans;
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(ll i=0;i<n;i++) cin>>a[i];
sort(a,a+n);
for(ll i=0;i<n;i++){
ans+=a[i]*(n-i-1);
}
cout<<ans<<endl;
}
|
AcWing104 货舱选址
题意
思路
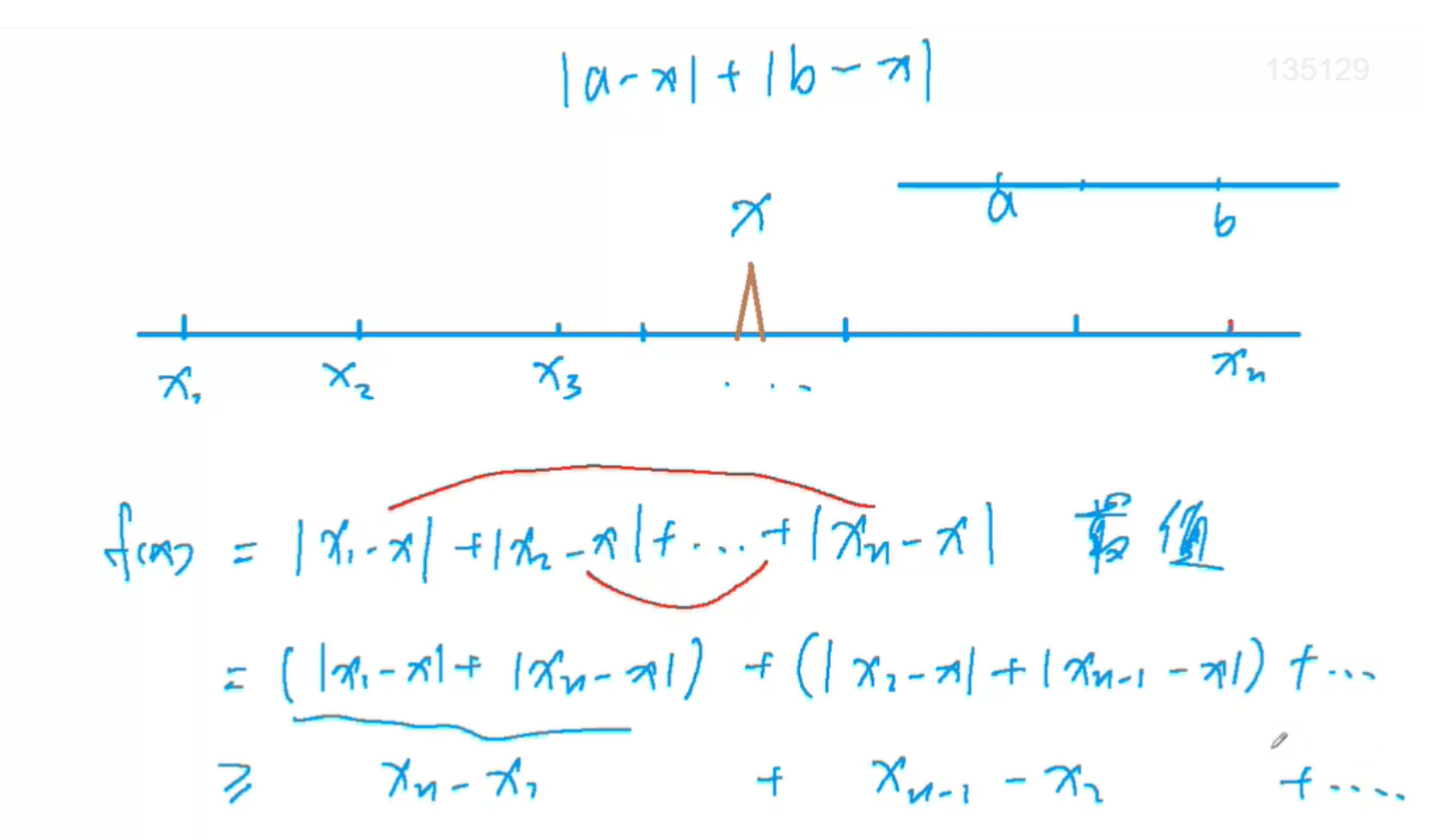
代码
绝对值不等式
AcWing104 货仓选址
题意
数轴上N个坐标,求一个坐标到每个坐标的距离之和最小,求距离最小值
思路
这个点在中间
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll n,ans;
int a[N];
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
sort(a,a+n);
for(int i=0;i<n/2;i++){
ans+=abs(a[n-1-i]-a[i]);
}
cout<<ans<<endl;
}
|
其他类型
AcWing1055 股票购买
题意
长度为 N数组,第 i个数字表示一个给定股票在第 i天的价格。
计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
思路
低买高出就行
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,ans;
int a[N];
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<n;i++){
if(a[i]<a[i+1]){
ans+=a[i+1]-a[i];
}
}
cout<<ans<<endl;
}
|





