【SE】数学基础知识

• 高数、线代、概率论一些常用基础知识点复习

重点复习

• 线代部分

• 矩阵中秩和迹是如何计算的，物理意义分别是什么？秩是什么？什么是矩阵满秩？怎么求矩阵的秩？

• 什么是线性变换？什么是线性空间？
• 什么是全等变换？
• 什么是极大无关组？
• 什么是矩阵相似？
• 正定矩阵是什么？
• 正交矩阵的定义
• 什么是矩阵合同
• 对称矩阵是什么？
• 特征值和特征向量几何含义？它们的意义以及之间的关系
• 矩阵可逆的条件？
• 子空间是什么？
• 描述一下特征值分解？
• 行列式的几何意义？
• 线代：如何理解矩阵的秩？简述向量组线性无关的含义？解释正定矩阵以及半正定矩阵？特征值的含义以及矩阵分解的物理意义？

概率论部分

• 解释什么是大数定理，有什么用，什么时候用？
• 解释什么是中心极限定理，有什么用，怎么用？数据如何处理？
• 全概率公式怎么写？
• 贝叶斯公式与应用？
• 介绍下正态分布，正态分布的和还是正态分布吗，正态分布性质与独立同分布）
• 解释下相关系数、协方差。相关系数或协方差为0的时候能否说明两个分布无关？为什么？
• 极大似然估计
• 独立和不相关的区别

离散数学部分

• 偏序关系和等价关系
• 解释下等价关系和等价类
• 双射
• 什么是覆盖和划分、偏序集合、强弱连通图

线性代数

参考阅读：

矩阵乘法核心思想（1）：列空间 - 知乎 (zhihu.com)

线性变换

🔴 $\textcolor{red}{线性变换}$

$$\begin{array}{c} L(\overrightarrow{\mathbf{v}}+\overrightarrow{\mathbf{w}})=L(\overrightarrow{\mathbf{v}})+L(\overrightarrow{\mathbf{w}}) \\ L(c \overrightarrow{\mathbf{v}})=c L(\overrightarrow{\mathbf{v}}) \end{array}$$

几何角度理解：它是网格线保持平行且等距分布的变换（1）直线在变换后仍保持直线，不弯曲 （2）原点必须固定

一种矩阵相乘的几何理解方式👉线性变换作用于给定向量：把矩阵的列看作变换后的基向量，矩阵向量乘法看作它们的线性组合

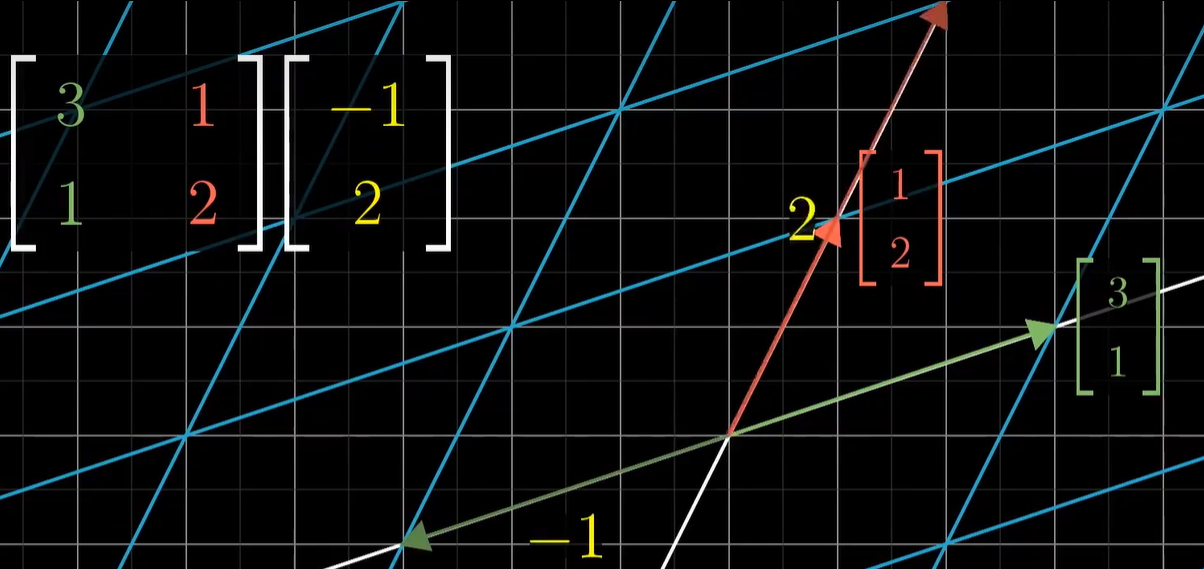
线性相关和线性无关

🔴 $\textcolor{red}{张成空间}$

所有可以表示为给定向量 线性组合 的向量的集合，被称为给定向量的张成空间

仅通过向量加法和数乘，所能获得的可能向量的集合

🔴 $\textcolor{red}{线性组合}$

m个n维向量$\alpha_{1},\alpha_{2},…,\alpha_{m}$，及m个数$k_{1},k_{2},…,k_{m}$，则向量$k_{1}\alpha_{1}+k_{2}\alpha_{2}+…+k_{m}\alpha_{m}$称为向量$\alpha_{1},\alpha_{2},…,\alpha_{m}$的一个线性组合

多个数乘向量的和

线性是指向量乘以一个标量，沿着向量的方向缩放，方向不变；组合是把多个向量加起来

🔴 $\textcolor{red}{线性相关和线性无关}$

对m个n维向量$\alpha_{1},\alpha_{2},…,\alpha_{m}$，若存在不全为0的数$k_{1},k_{2},…,k_{m}$，使得$k_{1}\alpha_{1}+k_{2}\alpha_{2}+…+k_{m}\alpha_{m}=0$成立，则称$\alpha_{1},\alpha_{2},…,\alpha_{m}$线性相关，否则称线性无关

或者说，一个向量可以表示为其他向量的线性组合，那么这些向量线性相关

几何角度理解：

• 线性相关：一组向量中至少有一个是多余的，没有对张成空间做出贡献，可以移除其中一个而不减小张成空间

• 线性无关：一组向量中的所有向量都给张成空间增添了新的维度

  比如对于$\vec a$ 和$\vec b$ 张成的二维平面，若$\vec c$ 刚好落在该平面中，那么$\vec c$ 的加入对张成空间没有任何贡献，仍然是一个二维平面，说明它们三个是线性相关的；如果$\vec c$ 没有落在那个二维平面，而使得张成空间变成一个三维空间了，说明它们三个是线性无关的

• 或者说：一组矢量的线性相关性本质上，是描述他们所张成的广义平行四边形体积是否为零。N个向量线性无关👉他们所张成的N维体的体积不为零。于是有：线性无关矢量组成的矩阵的行列式不为零；线性相关矢量组成的矩阵的行列式必为零。

🔴 $\textcolor{red}{空间中的一组基}$

向量空间中的一组基是张成该空间的一个线性无关的向量集合

行列式

🔴 $\textcolor{red}{行列式的几何意义}$

可以理解为线性变换的比例，如果是负数，说明变换后的空间定向发生改变

例如，一个线性变换作用于一个2x2矩阵，该线性变换的行列式是1/2，那么变换后的区域的面积变成了原来的1/2（三维则是体积的缩放）；

若一个二维线性变换的行列式为0，说明它将整个平面压缩到一条线，甚至一个点上，👉根据行列式是否=0，就能知道这个矩阵所代表的变换是否将空间压缩到更小的维度上

或者理解为：向量围成空间的面积或体积；行列式就是在给定一组基下，N个向量张成的一个N维广义四边形的体积。2阶行列式代表的是平面内的面积；3阶行列式自然而然就是3维空间内的体积；4阶行列式是4维空间里的超体积

矩阵

基本概念

🔴 $\textcolor{red}{逆矩阵}$

理论定义：

理解：$Ax=v $ ⇨ $A^{-1}Ax=A^{-1}v$ ⇨ $x=A^{-1}v$

寻找一个向量$x$，使得它在经过线性变换$A$ 之后与 $v$ 重合：$Ax=v$

• 若行列式$|A|=0$，说明线性变换$A$ 将空间压缩到了更低维度→ 不存在$A^{-1}$
• 若$|A|\neq 0$（← 矩阵可逆的充要条件），说明原来的空间没被挤压，在这种情况下，有且仅有一个向量$x$在变换后与$v$重合

即便不存在$A^{-1}$，解仍然可能存在：$A$将空间压缩为一条直线，而原本的$v$也刚好落在这条直线上

🔴 $\textcolor{red}{秩}$

理论定义：

几何角度理解：代表变换后的维数

若一个线性变换作用的结果是一维的，则这个变换的秩是1，二维的则是2…

一个3x3的矩阵，秩=2，说明空间被压缩

🔴 $\textcolor{red}{列空间}$

所有可能的输出向量$Av$构成的集合称作$A$的列空间（矩阵的列所张成的空间）；

更精确地讲，秩是列空间的维数

用于线性变换的矩阵的列 可以看作 变换后的基向量，这些变换后的基向量张成的空间就是所有可能的变换结果

🔴 $\textcolor{red}{满秩}$

对于一个满秩变换：唯一能在变换后落在原来的点就是零向量本身；

对于非满秩变换，它将空间压缩到一个更低的维度上⇨ 会有一系列在变换后称为零向量

一个二维线性变换将空间压缩到一条直线上，那么沿着某个不同于该直线的方向的所有向量都被压缩到原点

零空间（核）：变换后会落在原点的向量的集合；对于$Ax=0$，零空间给出了这个向量方程所有可能的解

各种矩阵

🔴 $\textcolor{red}{正定矩阵}$

🔴 $\textcolor{red}{正交矩阵}$

🔴 $\textcolor{red}{对称矩阵}$

🔴 $\textcolor{red}{矩阵合同}$

🔴 $\textcolor{red}{相似矩阵}$

内积和外积

点积（点乘），叉积（叉乘）

内积

🔴 $\textcolor{red}{定义}$

设有$n$维向量，$x=\begin{pmatrix}x_1\\ x_2\\ \vdots\\ x_n\end{pmatrix}$，$y=\begin{pmatrix}y_1 \\y_2\\ \vdots \\y_n\end{pmatrix}$，$x$和$y$的内积 $x \bullet y$ 如下：

$$x^{T} y=\left(x_{1}, x_{2}, \cdots, x_{n}\right)\left(\begin{array}{c}y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{array}\right)=x_1y_1+x_2y_2+...+x_ny_n$$

🔴 $\textcolor{red}{几何意义}$

$v\cdot w$的结果：$w$在$v$上的投影长度 乘 $v$的长度： $|w||v|cos \theta$

外积

外积的结果是一个向量，并非一个数

以二维为例，结果就是两个向量围成的平行四边形的面积

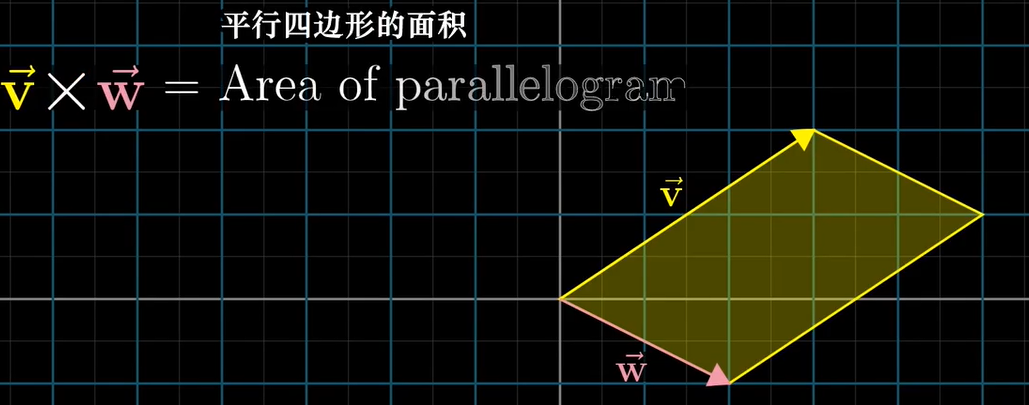
面积的计算可以考虑行列式、$|v\times w| =|v||w|sin\theta$

方向的确定（基向量的确定就是定向的基础）：

真正的叉积是两个三维向量生成一个新的三维向量

方向的确定（右手定则）：

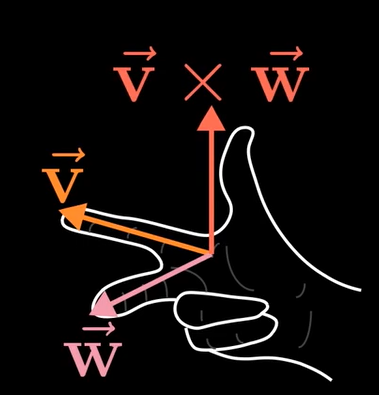
计算：

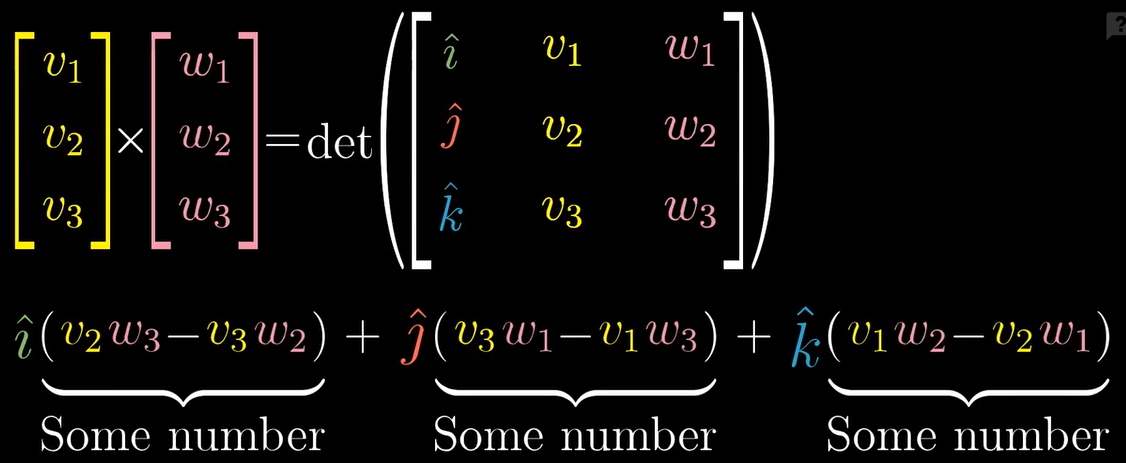
特征值和特征向量

🔴 $\textcolor{red}{定义}$

给定一个矩阵$A$，寻找一个常数$\lambda$和一个非零向量$x$ ，使得向量$x$被矩阵$A$作用后所得到的向量$Ax$ 与 原向量$x$ 平行，并且满足$Ax = \lambda x$ 。那么，$\lambda$：特征值，$x$：特征向量。

求特征向量：$Ax=\lambda Ix$ （$I$是单位对角阵），$(A-\lambda I)x=0$，$x$是非零向量，因为当且仅当矩阵代表的变换将空间压缩到更低维度时，才会存在一个非零向量，使得矩阵和它的乘积为0，所以最终就是求行列式$|A-\lambda I|=0$

🔴 $\textcolor{red}{理解}$

几何角度理解：

• 将一个线性变换施加在一个基上，线性变换后仍然留在原来的基所张成的空间里的向量，就是这个线性变换的特征向量，任何其他向量在变换中都有或多或少的旋转→离开它原来张成的那条直线。
• 每个特征向量都有一个所属的值：特征值，它是用来衡量特征向量在线性变换中拉伸或压缩比例的因子。

例如某特征向量的特征值是-1/2，意味着原向量被反向且压缩为原来的1/2，但它仍然留在原来张成的直线上，并为发生旋转。

考虑一个三维空间的旋转，若能找到这个旋转的特征向量，也就相当于找到了它的旋转轴，这种情况下，相应的特征值=1：旋转不缩放任何一个向量

特征值越大，我们可以认为对应的特征向量越重要。既然特征值表达了重要程度且和特征向量所对应，那么特征值大的就是主要信息，基于这点我们可以提取各种有价值的信息。

🔴 $\textcolor{red}{特征空间}$

特征空间包含了所有的特征向量

🔴 $\textcolor{red}{基变换}$

数据与第一个基做内积运算，结果为第一个新的坐标分量，依次类推，例如数据$(3,2)$映射到给定的一个基上的坐标：

$$\begin{pmatrix}1/\sqrt2 &1/\sqrt2 \\-1/\sqrt2 &1/\sqrt2 \end{pmatrix}\begin{pmatrix}3 \\2 \end{pmatrix}=\begin{pmatrix}5/\sqrt[]{2} \\-1/\sqrt[]{2} \end{pmatrix}$$

特征值分解

---

概率论与梳理统计

大数定律和中心极限定理

中心极限定理是说无论抽样分布如何 均值服从正态分布 ，而大数定律根本和正态分布无关 是说样本大了抽样分布近似总体分布

参考阅读：

大数定理的通俗理解_haso的博客-CSDN博客

怎样理解和区分中心极限定理与大数定律？ - 知乎 (zhihu.com)

大数定律具体是个什么概念？ - 知乎 (zhihu.com)

大数定律

🔴 $\textcolor{red}{关键理解}$

• 小数定律：如果统计数据很少，那么事件就表现为各种极端情况，而这些情况都是偶然事件，跟它的期望值一点关系都没有

• 大数定律：在试验不变的条件下，重复试验多次，那么随机事件出现的频率就能无限接近它的期望值（概率）。因此我们可以用样本均值来估计总体的期望。

🔴 $\textcolor{red}{切比雪夫大数定律(一般情形)}$

设$ X_{1}, X_{2}, \ldots, X_{n}, \ldots $是由两两不相关（或两两独立）的随机变量所构成的序列, 分别具有 数学期望$E\left(X_{1}\right), E\left(X_{2}\right), \ldots, E\left(X_{n}\right), \ldots $和方差$D\left(X_{1}\right), D\left(X_{2}\right), \ldots D\left(X_{n}\right), \ldots ,$ 并且方差 有公共上界, 即存在正数 $M$ , 使得 $D\left(X_{n}\right) \leq M, n=1,2, \ldots ,$则对于任意给定的正数 $\varepsilon$ 总有：

$$\lim _{n \rightarrow \infty} P\left\{\left|\frac{1}{n} \sum_{k=1}^{n} X_{k}-\frac{1}{n} \sum_{k=1}^{n} E X_{k}\right|<\varepsilon\right\}=1$$

这些变量的均值 依概率收敛为 这些期望的均值

🔴 $\textcolor{red}{独立同分布的切比雪夫大数定律(特殊情形)}$

设随机变量$X_{1}, X_{2}, \ldots, X_{n}, \ldots$相互独立, 服从相同的分布, 具有数学期望$E\left(X_{n}\right)=\mu$ 和 方差$D\left(X_{n}\right)=\sigma^{2}(n=1,2, \ldots)$，则对于任意给定的正数$\varepsilon$，总有：

$$\lim _{n \rightarrow \infty} P\left\{\left|\frac{1}{n} \sum_{k=1}^{n} X_{k}-\mu\right|<\varepsilon\right\}=1 ,即随机变量序列 \overline{X_{n}}=\frac{1}{n} \sum_{k=1}^{n} X_{k} \stackrel{P}{\longrightarrow} \mu .$$

🔴 $\textcolor{red}{辛钦大数定律}$

设随机变量$X_{1}, X_{2}, \ldots, X_{n}, \ldots$相互独立, 服从相同的分布，具有数学期望$E\left(X_{n}\right)=\mu (n=1,2, \ldots)$，则对于任意给定的正数$\varepsilon$，总有

$$\lim _{n \rightarrow \infty} P\left\{\left|\frac{1}{n} \sum_{k=1}^{n} X_{k}-\mu\right|<\varepsilon\right\}=1$$

🔴 $\textcolor{red}{伯努利大数定律}$

它的直观表达就是只要做的试验够多，出现的次数 除以 总次数的结果 接近 统计概率p

设在每次实验中$A$发生的概率$P(A)=p$，在$n$次独立重复实验中，事件$A$发生的频率为$f_n(A)$，则对任意正数$\varepsilon$，总有：

$$\lim _{n \rightarrow \infty} P\left\{\left|f_n(A)-p\right|<\varepsilon\right\}=1$$

中心极限定理

参考视频：中心极限定理的直观理解_哔哩哔哩_bilibili

🔴 $\textcolor{red}{关键理解}$

• 中心极限定理告诉我们，当样本量足够大时，样本均值的抽样分布慢慢趋近于正态分布

• 不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布

🔴 $\textcolor{red}{棣莫弗-拉普拉斯中心极限定理}$

设随机变量$X_n$服从参数$n$和$p$的二项分布，即$X_n\sim B(n,p)(0<p<1,n=1,2,\dots)$，则对于任意实数$x$，有：

$$\lim _{n \rightarrow \infty} P\left\{\frac{X_{n}-n p}{\sqrt{n p(1-p)}} \leq x\right\}=\Phi(x)$$

$\Phi(x)$为标准正态分布的分布函数

🔴 $\textcolor{red}{列维-林德伯格中心极限定理}$

设随机变量$X_{1}, X_{2}, \ldots, X_{n}, \ldots$相互独立, 服从相同的分布, 具有数学期望$E\left(X_{n}\right)=\mu$ 和 方差$D\left(X_{n}\right)=\sigma^{2}(n=1,2, \ldots)$，则对于任意实数$x$，有：

$$\lim _{n \rightarrow \infty} P\left\{\frac{\sum_{k=1}^{n} X_{k}-n \mu}{\sqrt{n} \sigma} \leq x\right\}=\Phi(x)$$

$\Phi(x)$为标准正态分布的分布函数

全概率公式和贝叶斯公式

各种分布

协方差和相关系数

离散数学

群论

参考阅读：

【群论入门】(2)：模算术 - 知乎 (zhihu.com)

【群论入门】(3): 群的定义 - 知乎 (zhihu.com)

【近代应用数学-南京大学】给非数学系的基础入门款 群论/实变/点集拓扑/泛函_哔哩哔哩_bilibili

基本定义

🔴 $\textcolor{red}{代数运算}$

设$A$非空集合，引入一个法则，使得$A$中任意两个元素与$A$中另一个元素唯一对应，那么可以把这个法则称为$A$上的一个代数运算

例如：A是实数集合$\mathbb{R}$，法则→加法$+$；$\forall x,y\in \mathbb{R}$，$x+y\in \mathbb{R}$。

又如：向量的内积就不是一个代数运算，$\vec a,\vec b\in V$，$\vec a \cdot \vec b \in \mathbb{R}$，也就是说$V\cdot V\to \mathbb{R}$

🔴 $\textcolor{red}{半群}$

设$(S，∗)$ 是一个代数系统，“∗”是非空集合S上的一个代数运算。若

​ （1）“∗”具有封闭性，即∗是S上的闭运算； （2）“∗”满足结合律。

则称(S，∗)是一个半群。

比如，G={2，4，6，8，…}，（G,+)就是一个半群，只满足结合律，没有幺元0，也没有逆元负数

🔴 $\textcolor{red}{幺元}$

设$(S，∗)$是一个代数系统，

（1）若存在$e_右∈S$，使得对于任意的$x∈S$，有$x∗e_右=x$，则称$e_右$是右幺元。

（2）若存在$e_左∈S$，使得对于任意的$x∈S$，有$e_左∗x=x$，则称$e_ 左$是左幺元。

（3）若存在一个元素e∈S，它既是左幺元，又是右幺元，则称e是幺元（又称单位元）。

若有幺元，则幺元唯一。

证明：设$e_左，e_右∈S$分别是左幺元和右幺元，则有$e_左=e_左∗e_右=e_右$

若有$e_1，e_2∈S$，且均是幺元，则有$e_1=e_1∗e_2=e_2$通常用$e$表示么元

🔴 $\textcolor{red}{含幺半群}$

称含有幺元的半群为含幺半群。

比如 0是半群$(N，+)$的幺元，而1是半群$(N，×)$的幺元。$(N，+)$和$(N，×)$都是含幺半群

子半群：设$(S，∗)$是一个半群，$∅≠A⊆S$，若$(A，∗)$本身是一个半群，则称$(A，∗)$是$(S，∗)$的子半群

比如：G={0，2，4，6，8，…}，（G,+)就是一个幺半群，满足结合律，有幺元0，也没有逆元负数

若，G={0，±1，±2，…}，(G,+)就是一个群；

最小的群：（G,$\circ$) = {e}

🔴 $\textcolor{red}{逆元}$

设$(S，∗)$是一个代数系统，$e∈S$是幺元，$a∈S$。

（1）若存在$b∈S$，使得$a∗b=e$，则称$b$是$a$的右逆元；

（2）若存在$d∈S$，使得$d∗a=e$，则称$d$是$a$的左逆元；

（3）若存在$a^′∈S$，使得$a^′$既是$ a$的左逆元，又是$a$的右逆元，则称$a^′$是$a$的逆元。

设(S，∗)是一个代数系统，∗满足结合律，e∈S是幺元，a∈S是任意的元素，则

（1）若a既有左逆元，又有右逆元，则a的左逆元等于右逆元，即为a的逆元。

（2）a的逆元若存在，则唯一。

🔴 $\textcolor{red}{群的定义}$

$(S，∗)$是一个代数系统，若$(S，∗)$满足以下四条：

（1）”∗”是$S$上的闭运算；

（2）”∗”适合结合律；

（3）存在幺元$e∈S$（又称之为单位元）；

（4）对于$S$中的任意元素$a$，存在逆元$a^{−1}∈S$。

则称$(S，∗)$是一个群。

半群：(1)+(2)；幺半群：(1)+(2)+(3)

🔴 $\textcolor{red}{左右消去律}$

设$(S，∙)$是一个代数系统。若对于任意的$x，y，z∈S$，满足

如果$x∙y=x∙z$，那么$y=z$，则称“$∙$”运算满足左消去律；

如果$y∙x=z∙x$，那么$y=z$，则称“$∙$”运算满足右消去律。

设$(G，∙)$是一个群，则“$∙$”运算分别满足左、右消去律

🔴 $\textcolor{red}{群的性质}$

🔸 群$(G,\circ)$，若$a,b\in G$，$b\circ a=e$，则$a\circ b=e$

🔸 群$(G,\circ)$，$e$，$\forall a\in G$，$e\circ a=a\circ e =a$

🔸 群$(G,\circ)$ 的幺元 $e$ 是唯一的

🔸 群$(G,\circ)$ ，$\forall a\in G$，$a$ 的逆元是唯一的

🔴 $\textcolor{red}{幂}$

$a\in G,n\in \mathbb{N},a^n=a…a,\quad a^0=e,a^{-1}=a的逆元，(a^{-1})^n = a^{-n}$

∴ $a^{m+n}=a^m \circ a^n,m、n\in \mathbb{Z}$

∴ $(a^n)^m = a^{nm}$

🔴 $\textcolor{red}{阶}$

群$(G,\circ)$，$a\in G$，$a^m=e$的最小的$m\in \mathbb{N}$，$m$称为$a$的阶，若找不到$m\in \mathbb{N}$，称$a$的阶为0

群的同态和同构

🔴 $\textcolor{red}{同态和同构}$

设$(S_1，∗)$，$(S_2，∙)$是两个代数系统，“∗” 是$S_1$上的一个二元运算，“∙” 是$S_2$上的一个二元运算。设$f$是$S_1$到$S_2$的一个映射，即$f：S_1→S_2$。若对于$S_1$中的任意两个元素$x_1，x_2$，有$f(x_1∗x_2)=f(x_1)∙f(x_2)$，则称映射$f$是$S_1到S_2$的一个同态映射。

• 若$f$是单射，则称$f$是一个单一同态映射；
• 若$f$是满射，则称$f$是一个满同态映射；
• 若$f$是双射，则称$f$是一个同构映射。

若两个代数系统之间存在一个同构映射，则称这两个代数系统是同构的。

群的同构作为群的关系，是一个等价关系：满足自反性、对称性、传递性

🔴 $\textcolor{red}{例子}$

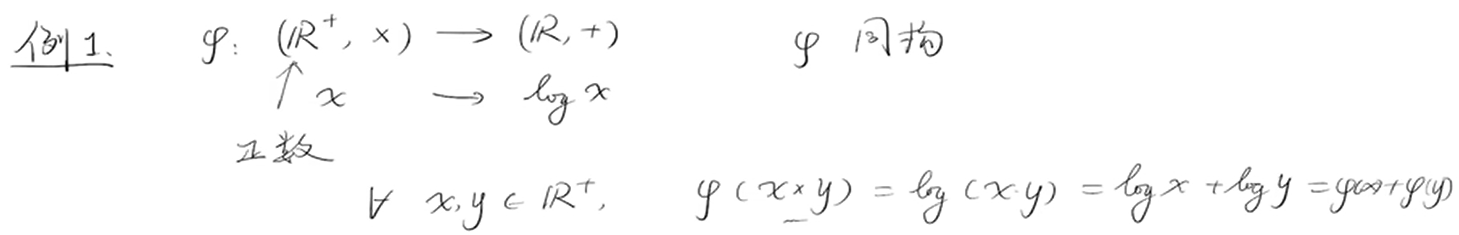
无限群和有限群

🔴 $\textcolor{red}{定义}$

设$(G，∙)$是一个群，

若$G$是无限集，则称$(G，∙)$是无限群。

若$G$是有限集，且$|G|=n$，则称$(G，∙)$是$n$阶有限群。

🔴 $\textcolor{red}{阶}$

比如：在整数加群$(Z，+$)中，对于任意的$a∈Z(a≠0)$，因为对于任意的正整数n，有$a+a+⋯+a(n个a)=na≠0$ 所以，$o(a)=∞$

设$(G，∙)$是一个交换群，对于任意的$ a，b∈G$，有$(a∙b)^n=a^n∙b^n$。

交换群（阿贝尔群）

对于$G$中任意两个元素$a，b∈G$，若满足交换律$，a∙b=b∙a$，则称$(G，∙)$是交换群，又称阿贝尔（Abel）群

变换群 置换群 循环群

🔴 $\textcolor{red}{集合的变换}$

$A$非空集合，称由$A$到自身的映射$\tau：A\to A$ 称为集合上的一个变换，记为：$a\in A\to \tau(a)\in A$

满变换、单变换、一一变换

把集合$A$上的全体变换作成集合$S=\{\tau,\lambda,\mu,\dots\}$，规定$S$上的一个代数运算$\circ$，$\forall \tau,\lambda\in S，\tau :a\to\tau(a);\lambda:a\to\lambda(a)$， 将$\lambda \circ \tau$定义为：$a\to \lambda(\tau(a))$。（也就是两个变换的复合）

这个“乘法“满足结合律：$\forall \tau,\lambda,\mu\in S，\tau(\lambda\mu)=(\tau\lambda)\mu $

🔴 $\textcolor{red}{变换群}$

设$A$是一个非空集合，$G$是由$A$到$A$的一些映射构成的集合，若$G$是关于运算“$∘$”构成的一个群，则称$(G，∘)$是集合$A$上的一个变换群。

🔴 $\textcolor{red}{Cayley定理}$

任何一个群都与一个变换群同构

🔴 $\textcolor{red}{置换群}$

设$A$是一个非空有限集，则

（1）称$A$上的一个变换群为$A$上的一个置换群。

（2）对于任意的$f∈∪(A^A)$，称$f$为集合$A$上的一个置换。

🔴 $\textcolor{red}{循环群}$

设$(G，∙)$是一个群，$g∈G$。若$G$中每一个元素都是$g$的乘方，则称$G$为循环群，称$g$为生成元，并且用符号$G=(g)$表示，即$G=(g)={g^n│n∈Z}$。

设$(G，∙)$是一个群，$g∈G$ ，

显然有$g^2∈G，g^3∈G，⋯$，即对于任意的正整数$n$，有$g^n∈G$；

显然有$g^{−1}∈G，g^{−2}∈G，⋯$，即对于任意的正整数$n$，有$g^−n∈G$；

规定$g^0∈G$是$G$中幺元。

综上所述，对于任意整数$n∈Z，g^n∈G$。 显然，$({g^n│n∈Z}，∙)$是一个群。

设$G=(g)$是一个循环群，如果$o(g)=n$，则$|G|=n$，且$G=(g)=\{g^0=e，g，g^2，⋯，g^{n−1}\}$

（1）若$o(g)=n$，则称$G$是$n$阶有限循环群。 （2）若$o(g)=∞$，则称$G$是无限循环群

子群

🔴 $\textcolor{red}{子群定义}$

设$(G，∙)$是一个群，$∅≠A⊆G$，若$(A，∙)$也是一个群，则称$(A，∙)$$是(G，∙)$的子群。

子群的陪集

🔴 $\textcolor{red}{右陪集}$

设$(G，∙)$是一个群，$(H，∙)$是$(G，∙)$的一个子群，$a∈G$。称$H∙a=\{ℎ∙a|ℎ∈H\}$为子群$H$的右陪集

🔴 $\textcolor{red}{左陪集}$

设$(G，∙)$是一个群，$(H，∙)$是$(G，∙)$的一个子群，$a∈G$。称$a∙H=\{a∙h|ℎ∈H\}$为子群$H$的左陪集

正规子群和商群

🔴 $\textcolor{red}{正规子群}$

设$G$是一个群，$H$是$G$的一个子群。若对于任意一个$a∈G$，有$a∙H=H∙a$即$a$关于$H$的左陪集等于右陪集，则称$H$是$G$的正规子群，或者称为不变子群

🔴 $\textcolor{red}{商群}$

设$G$是一个群，$H$是$G$的正规子群，$G/H=\{aH|a∈G\}$，对于任意的$aH$，$bH∈G/H$，$(aH)⊙(bH)=(ab)H$。则$(G/H，⊙)$是一个群。该群称为$G$的商群。

图论