【机器学习】支持向量机SVM

支持向量机

SVM（支持向量机）

参考文献链接：

2.1.1]—支持向量机（线性可分定义）_哔哩哔哩_bilibili （b站上 浙江大学胡浩基老师的讲解视频）

【机器学习】支持向量机 SVM（非常详细） - 知乎 (zhihu.com)

机器学习算法（一）SVM_yaoyz105的博客

【机器学习算法笔记系列】支持向量机(SVM)算法详解和实战_fpzRobert的博客

简介

机器学习的一般框架：
训练集 => 提取特征向量 => 结合一定的算法（分类器：比如决策树、KNN）=>得到结果

阐述

SVM是二分类模型，将实例的特征向量 映射成空间中的一些点，寻找一个超平面来对样本点进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解，若出现新的点，这个超平面也能做出很好的分类

• 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机
• 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机
• 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机

优缺点

优点

• 决策函数只由少数的支持向量决定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了维数灾难。
• 可进行小样本学习：支持向量机(SVM)本质上是非线性方法，在样本量比较少的时候，容易抓住数据与特征之间的非线性关系，因此可以解决非线性问题、可以避免神经网络结构选择和局部极小值点问题、可以提高泛化能力、可以解决高维问题。（分类鲁棒性高、全局最优解）

缺点

• 对大规模训练样本难以实施，由于SVM是借助二次规划来求解支持向量，而求解二次规划将涉及m阶矩阵的计算（m为样本的个数），当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。
• 原始分类器不加修改仅适用于处理二分类问题（改进：通过多个二类支持向量机的组合来解决等等）
• 对缺失数据敏感，对参数调节和核函数的选择敏感。对非线性问题没有通用解决方案，必须谨慎选择核函数来处理。

线性可分、不可分

在二维空间下，

• 线性可分Liner Separable

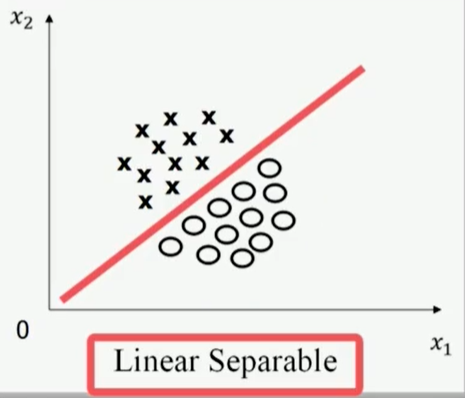
• 非线性可分NonLinear Separable：不存在一条直线

  

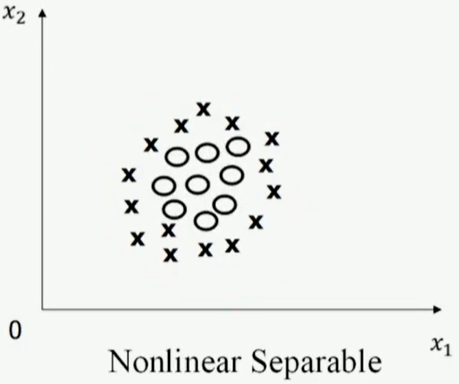
同理，在三维空间下，

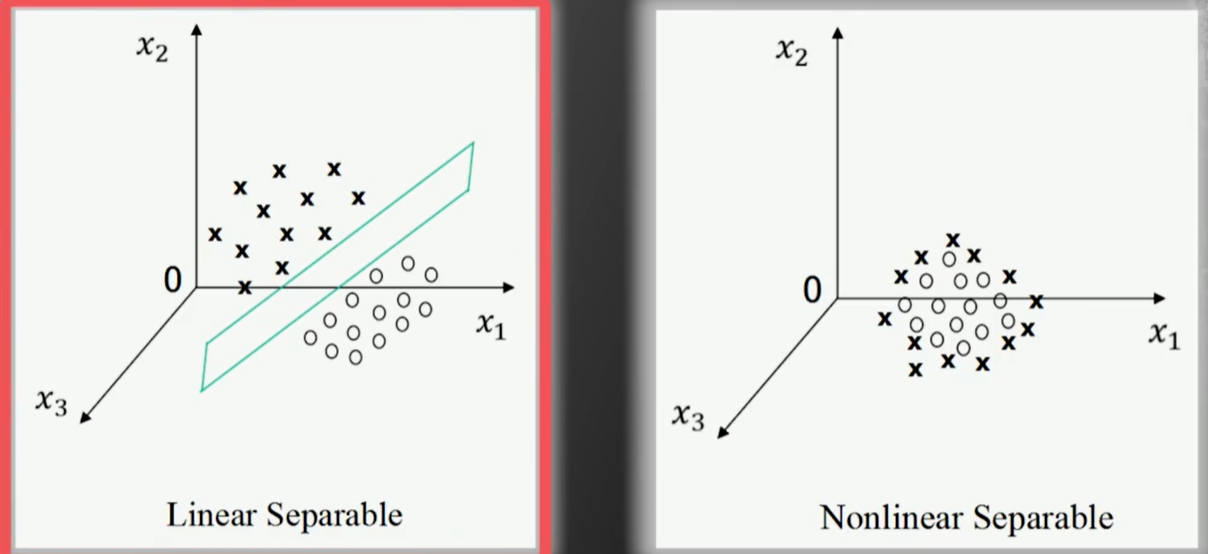
接下来看下图，

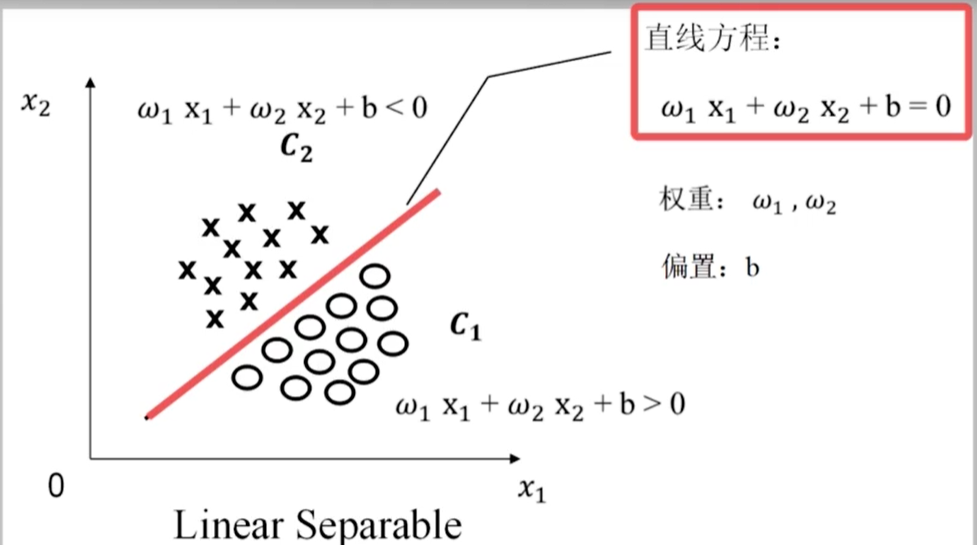
用数学严格定义训练样本以及他们的标签，假设，有N个训练样本及其标签$\left\{\left(X_{1}, y_{1}\right),\left(X_{2}, y_{2}\right), \ldots,\left(X_{N}, y_{N}\right)\right\}$，其中

$$\begin{aligned} X_{i} &=\left[x_{i 1}, x_{i 2}\right]^{T} \\ y_{i} &=\{+1,-1\} \end{aligned}$$

人为规定，如果$X_i$属于$C_1$，则$y_i$等于+1，若属于$C_2$，等于-1。

线性可分的严格定义：

​ 一个训练样本集$\left\{\left(X_{1}, y_{1}\right),\left(X_{2}, y_{2}\right), \ldots,\left(X_{N}, y_{N}\right)\right\}$，在$i=1 \to N$ 线性可分，是指存在$（w_1,w_2,b）$，使得

1. 若 $y_i = +1$ ，则 $\omega_{1} \mathrm{x}_{i 1}+\omega_{2} \mathrm{x}_{i 2}+\mathrm{b}>0$
2. 若 $y_i = -1$ ，则 $\omega_{1} \mathrm{x}_{i 1}+\omega_{2} \mathrm{x}_{i 2}+\mathrm{b}<0$

若用向量形式来定义，$X_{i}=\left[\begin{array}{l}
x_{i 1} \\
x_{i 2}
\end{array}\right]$，$\omega=\left[\begin{array}{l}
\omega_{1} \\
\omega_{2}
\end{array}\right]$，则有，

1. 若 $y_i = +1$ ，则 $\omega^{T} X_{i}+\mathrm{b}>0$
2. 若 $y_i = - 1$ ，则 $\omega^{T} X_{i}+\mathrm{b}<0$

最终线性可分的判定简化为：

$$\mathrm{y}_{i}\left(\omega^{T} X_{i}+b\right)>0$$

在二分类的情况下，如果一个数据集是线性可分的，即存在一个超平面将两个类别完全分开，那么一定存在无数多个超平面将这两个类别完全分开。

Q：为什么要叫作“超平面”呢？
A：样本的特征很可能是高维的，此时样本空间的划分就不是一条线

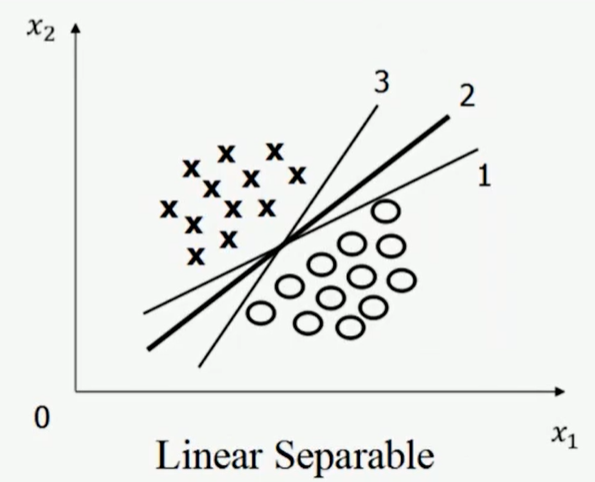
ヾ(,,・∇・,, 那么， 哪一个超平面最好呢？

Q：画线的标准是什么？/ 什么才叫这条线的效果好？/ 哪里好？
A：SVM 将会寻找可以区分两个类别并且能使间隔（margin）最大的划分超平面。比较好的划分超平面，样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。

Q：间隔（margin）是什么？
A：对于任意一个超平面，其两侧数据点都距离它有一个最小距离（垂直距离），这两个最小距离的和就是间隔。

Q：为什么要让 margin 尽量大？
A：因为大 margin 犯错的几率比较小，也就是更鲁棒啦。

问题描述

1、解决线性可分问题

2、将线性可分问题中获得的结论推广到线性不可分情况

将位于 上下两边的这两条平行线上的样本，称为 “支持向量”

这两条平行线之间的距离，称为“间隔”（Margin）

我们要找的，就是使得 间隔最大 的那条直线

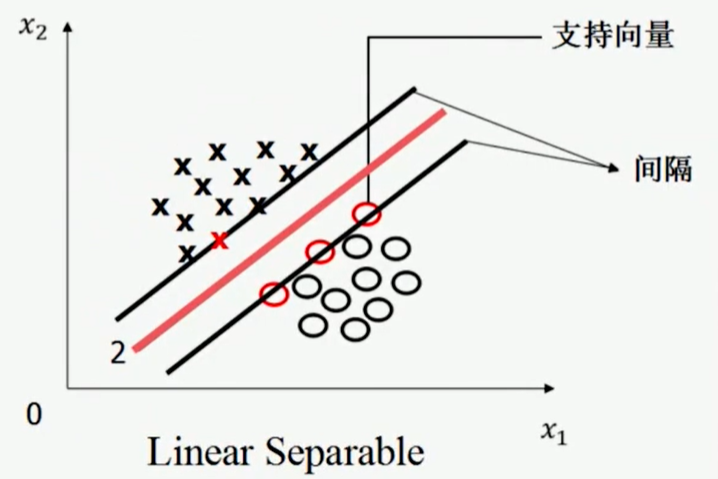
但是，使用“间隔最大”这条准则，并不能唯一的确定一条直线，因此，还需规定：这条线在上下两个平行线的中间

因此，SVM寻找的最优分类直线应该满足三个条件：

• 该直线分开了两类
• 该直线最大化间隔
• 该直线处于间隔的正中间，到所有支持向量距离相等

在线性可分的条件下，有且仅有唯一一条直线，满足上面三个条件。在高维空间中，直线就变成了超平面

优化问题（硬间隔）

用严格的数学，将寻找最优分类超平面的过程写成一个最优化问题

描述任意一个超平面：$w^{T} x+b=0$

$\omega=\left[\begin{array}{c}
\omega_{1} \\
\omega_{2} \\
\vdots \\
\omega_{m}
\end{array}\right]$，$|\omega|^{2}=\omega_{1}^{2}+\omega_{2}^{2} \ldots+\omega_{m}^{2}=\sum_{i=1}^{m} \omega_{i}^{2}$

点到直线距离：

• 二维空间：点 $(x,y)$ 到直线 $Ax+By+C=0$ 的距离：$\frac{|A x+B y+C|}{\sqrt{A^{2}+B^{2}}}$

• n维空间：点$x=\left(x_{1}, x_{2} \ldots x_{n}\right)$，到直线$w^{T} x+b=0$的距离：$\frac{\left|w^{T} x+b\right|}{|w|}$，其中$|w|=\sqrt{w_{1}^{2}+\ldots w_{n}^{2}}$

因此，支持向量到超平面的距离 若为$r$，则其它点到超平面的距离必然大于$r$。因此，对于所有样本点$x$：

$$\left\{\begin{array}{l} \frac{w^{T} x+b}{\|w\|} \geq r \quad y=1 \\ \frac{w^{T} x+b}{\|w\|} \leq-r \quad y=-1 \end{array}\right.$$

$|w|r$为正数，暂且令为$|w|r = 1$（方便推导，且对目标函数优化没有影响）

则为了$r$最大，则等价于：

$$\max _{w, b} \frac{1}{\|w\|} \Leftrightarrow \max _{w, b} \frac{1}{\|w\|^{2}} \Leftrightarrow \min _{w, b}\|w\|^{2} \Leftrightarrow \min _{w, b} \frac{1}{2}\|w\|^{2}$$

使得

$$\left\{\begin{array}{l} w^{T} x+b \geq 1 \quad y=1 \\ w^{T} x+b \leq-1 \quad y=-1 \end{array}\right.$$

上面这个方程组合并，简写为：

$$y\left(w^{T} x+b\right) \geq 1$$

故SVM最优化问题总结为：

已知：训练样本集$\{(X_i,y_i)\},i=1\to m$

待求：$(w,b)$

则可以表示为：$\min \frac{1}{2}|w|^{2} \text { s.t. } \quad y_{i}\left(w^{T} x_{i}+b\right) \geq 1 \quad i\in[1,m]$

凸优化（Convex Optimization）中的二次规划问题：

（1）目标函数是二次项

（2）限制条件是一次项

凸优化问题只有唯一一个全局极值，可用梯度下降求得

🔸 利用拉格朗日乘子法转换为对偶问题 求解超平面

原问题 写成 拉格朗日函数：

$$L(\omega, b, \alpha)=\frac{1}{2}\|\omega\|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\omega^{T} x_{i}+b\right)\right)$$

转换为 对偶问题

$$\max _{\alpha} \min _{w, b}L(w, b, \alpha) \quad s.t. \alpha_{i} \geq 0, \forall i \in\{1, \ldots m\}$$

同时要满足KKT条件（原问题可行、对偶问题可行、互补松弛）：

$$\begin{array}{cc} 1-y^{(i)}\left(\left(w^{*}\right)^{T} x^{(i)}+b^{*}\right) \leq 0 & \forall i \in\{1, \ldots m\} \\ \alpha_{i} \geq 0 & \forall i \in\{1, \ldots m\} \\ \alpha_{i}\left(1-y^{(i)}\left(\left(w^{*}\right)^{T} x^{(i)}+b^{*}\right)\right)=0 & \forall i \in\{1, \ldots m\} \end{array}$$

求解对偶问题：

• 拉格朗日函数最小化

  $$\begin{array}{c} \frac{\partial L(w, b, \alpha)}{\partial w}=w-\sum_{i=1}^{m} \alpha_{i} y^{(i)} x^{(i)}=0 \Rightarrow w=\sum_{i=1}^{m} \alpha_{i} y^{(i)} x^{(i)} \\ \frac{\partial L(w, b, \alpha)}{\partial b}=\sum_{i=1}^{m} \alpha_{i} y^{(i)}=0 \end{array}$$

  然后把上述结果带回到拉格朗日函数中，得到

  $$\min _{w, b} L(w, b, \alpha)=-\frac{1}{2} \sum_{i, j=1}^{m} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left(x^{(i)}\right)^{T} x^{(j)}+\sum_{i=1}^{m} \alpha_{i}$$

• 最大化 最小拉格朗日函数

  $$\begin{array}{c} \max _{\boldsymbol{\alpha}} \min _{\boldsymbol{w}, b} L(w, b, \alpha)=\max _{\alpha}\left(-\frac{1}{2} \sum_{i, j=1}^{m} y^{(i)} y^{(j)} \alpha_{i} \alpha_{j}\left(x^{(i)}\right)^{T} x^{(j)}+\sum_{i=1}^{m} \alpha_{i}\right) \\ \text { s.t. } \alpha_{i} \geq 0, \forall i \in\{1, \ldots m\} \\ \sum_{i=1}^{m} \alpha_{i} y^{(i)}=0 \end{array}$$

  通过序列最小优化SMO求解最优$\alpha^*$，则有：

  $$\boldsymbol{w}^{*}=\sum_{i=1}^{m} \alpha_{i}^{*} y^{(i)} x^{(i)}$$

  “有用的” $a^*>0$，根据KKT的互补松弛条件：

  $$\alpha_{i}^{*}\left(1-y^{(i)}\left(\left(w^{*}\right)^{T} x^{(i)}+b^{*}\right)\right)=0$$

  可知$1-y^{(i)}\left(\left(w^{}\right)^{T} x^{(i)}+b^{}\right)=0$，$(x^{(i)},y^{(i)})$一定是约束边界上的点，记为：$(\tilde{x},\tilde{y})$，因此有：

  $$b^{*}=\tilde{y}-w^{* T} \tilde{x}$$

  所以，SVM的决策函数为：

$$\hat{y}=\operatorname{sgn}\left(h_{w^{*}, b^{*}}(x)\right)=\operatorname{sgn}\left(\left(w^{*}\right)^{T} x+b\right)=\operatorname{sgn}\left(\sum_{i=1}^{m} \alpha_{i}^{*} y^{(i)}\left(x^{(i)}\right)^{T} x^{(i)}+b^{*}\right)$$

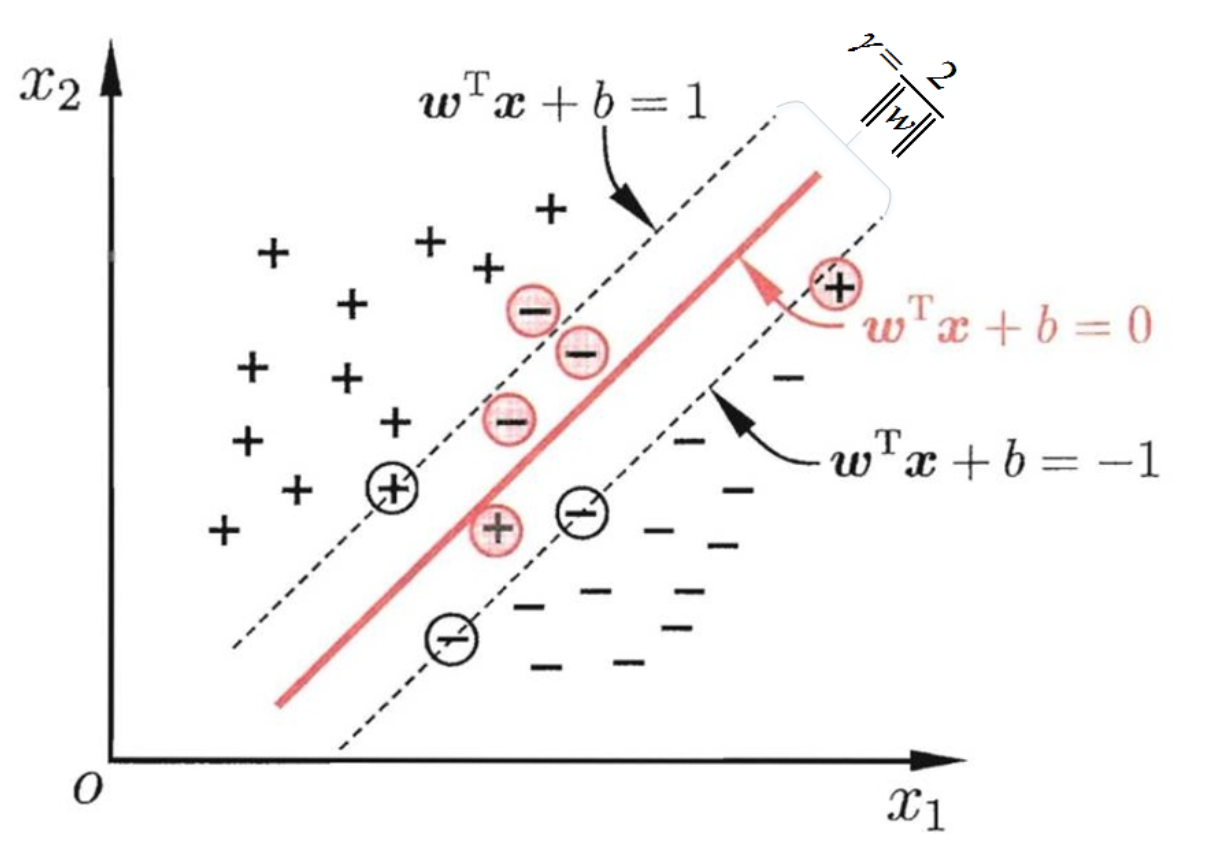
• 支持向量：满足$w^{T} x+b=1 \quad或\quad w^{T} x+b=-1$ 的点

• 每个支持向量到超平面的距离：$d=\frac{\left|w^{T} x+b\right|}{|w|}$

• 多维空间中任意平行的超平面间的距离：$\frac{|d_1-d_2|}{|w|}$

• 辅助决策边界距离：$2\frac{1}{|w|}$

线性不可分的情况（软间隔）

通常情况下，线性不可分的训练数据有一些特异点，去掉这些特异点后，剩下的大部分的样本点组成的集合是线性可分的。线性不可分意味着某些样本点不能满足间隔大于等于1的条件，样本点落在超平面与边界之间。

因此，需要适当放松限制条件，对于每个训练样本及标签，为每一个样本点设置松弛变量（slack variable）$\delta_{i}$

因此，限制条件改写为：

$$y_{i}\left(\omega^{T} X_{i}+b\right) \geq 1-\delta_{i},(i=1 \sim m)$$

再加入新的限制条件，防止松弛变量无限大，改造后SVM最优化版本如下：

最小化: $\frac{1}{2}|\omega|^{2}+C \sum_{i=1}^{N} \delta_{i} 或 \frac{1}{2}|\omega|^{2}+C \sum_{i=1}^{N} \delta_{i}^{2}$

限制条件

1. $\delta_{i} \geq 0 .(i=1 \sim m)$
2. $y_{i}\left(\omega^{T} X_{i}+b\right) \geq 1-\delta_{i},(i=1 \sim m)$

比例因子C是人为设定的——超参数

低维到高维的映射

把线性不可分转换成线性可分

把特征空间从低维映射到高维，用线性超平面对数据进行分类

对于原始样本空间不是线性可分的情况，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。

核函数的定义

核函数Kernel Function：

$$K\left(X_{1}, X_{2}\right)=\varphi\left(X_{1}\right)^{T} \varphi\left(X_{2}\right)$$

假设，$\varphi\left(X\right)$ 是一个将二维向量映射到三维向量的映射：

$$\begin{array}{c} X=\left[x_{1}, x_{2}\right]^{T} \\ \varphi(X)=\varphi\left(\left[x_{1}, x_{2}\right]^{T}\right)=\left[x_{1}^{2}, x_{1} x_{2}, x_{2}^{2}\right] \end{array}$$

假设有两个二维向量 $X_{1}=\left[x_{11}, x_{12}\right]^{T} \quad X_{2}=\left[x_{21}, x_{22}\right]^{T}$，根据上述定义，则有：

$$\varphi\left({X}_{1}\right)=\left[{x}_{11}^{2}, {x}_{11} {x}_{12}, {x}_{12}^{2}\right]\\ \varphi\left({X}_{2}\right)=\left[{x}_{21}^{2}, {x}_{21} {x}_{22}, {x}_{22}^{2}\right]$$

那么：

$$\begin{aligned} K\left(X_{1}, X_{2}\right) &=\varphi\left(X_{1}\right)^{T} \varphi\left(X_{2}\right) \\ &=\left[x_{11}^{2}, x_{11} x_{12}, x_{12}^{2}\right]\left[x_{21}^{2}, x_{21} x_{22} x_{22}^{2}\right]^{T} \\ &=x_{11}^{2} x_{21}^{2}+x_{11} x_{12} x_{21} x_{22}+x_{12}^{2} x_{22}^{2} \end{aligned}$$