高数基础知识

重点部分

可导、可微、连续、可积之间的关系（一元函数+二元函数）。✅
三个中值定理的区别、联系和物理意义（罗尔、拉格朗日、柯西），微分中值定理是啥？
如何求梯度？梯度、方向导数与梯度。✅
定积分如何求？定积分的意义？
给你一个物体表面离散的一堆点，如何求任意表面的法向量？
凸函数的定义，凸函数的局部最优解一定是全局最优解吗，为什么呢？
什么是数列的极限，也就是说一个数列xn，收敛于a，你如何定义它？
用数学语言描述极限
一阶导，二阶导的物理意义，几何意义
傅里叶级数和傅里叶变换的关系

高等数学

极限

函数

可微、可导、可积、连续

参考阅读：可微，可导，可积与连续的关系

一些定义

🔴 $\textcolor{red}{连续}$

设$y=f(x)$在$x_{0}$的某一邻域内有定义，若$\lim_{x \to \infty}f(x)= f(x_{0})$，则称$f(x)$在点$x_{0}$处连续

三个条件
- 函数在该点有定义
- 函数在该点极限$\lim_{x \to \infty}f(x)$存在
- 极限值 = 函数值：$\lim_{x \to \infty}f(x)= f(x_{0})$

🔴 $\textcolor{red}{可导}$

设$y=f(x)$在$x_{0}$的某一邻域$U(x_{0})$内有定义，当自变量$x$在$x_{0}$取得增量$\Delta x(x\neq 0) $，且$x_0 +\Delta x \in U(x_0)$时，相应的函数增量 $ \Delta y=f(x_0+\Delta x)-f(x_0)$，若极限

$\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}$

存在，则称函数在$x_0$处可导，并称这个极限值为函数在该点处的导数

🔴 $\textcolor{red}{可微}$

参考阅读：如何通俗理解全微分 - 知乎 (zhihu.com)

设函数$y=f(x)$ 在区间内有定义，$x_{0}$及$x_{0}+\Delta x$在区间内：

若增量 $ \Delta y=f(x_0+\Delta x)-f(x_0)$可表示为$\Delta y=A\Delta x+o(\Delta x)$
其中$A$是不依赖于$\Delta x$的常数，那么称函数$y=f(x)$ 在点$x_0$处可微。
$A\Delta x$ 叫做函数$y=f(x)$在点 $x_0$处相应于$\Delta x$的微分，记作$ \mathrm dy$

🔴 $\textcolor{red}{可积}$

$f(x)$在区间$[a,b]$上连续，则在$[a,b]$上可积
$f(x)$在区间$[a,b]$上有界，且只有有限个间断点，则在$[a,b]$上可积

联系【一元函数】

⭕ 可导必然连续，连续不一定可导

证明：连续性和可导性

例子：魏尔施特拉斯函数：处处连续而处处不可导：

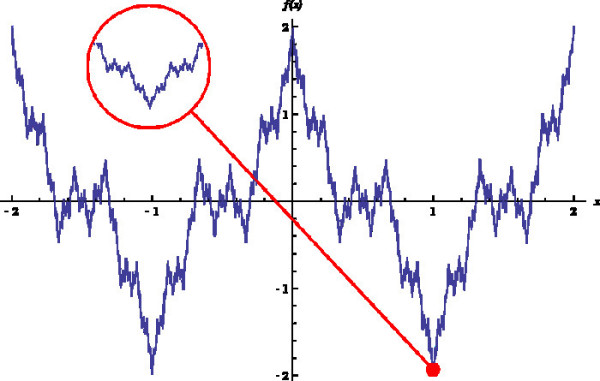
⭕ 可导和可微等价

一元函数和二元函数，可微和可导有什么区别？ - 知乎 (zhihu.com)

⭕ 连续必然可积，可积不一定连续

想想可积和连续的几何意义就理解了

⭕ 可导必然可积，可积不一定可导

可导👉连续👉可积，所以可导必可积。

可积不一定连续👉不一定可导，所以可积不一定可导。

联系【多元函数】

🔺 可导不一定连续，连续不一定可导

可导指的是可偏导，所以并不能推出在所有方向上函数连续

🔺 可微必然可导，可导不一定可微

一元函数👉可导：存在导数，可微：存在微分。

多元函数👉可导：存在偏导数，可微：存在全微分。

🔺可微必然连续，连续不一定可微

🔺偏导数连续必然可微，可微不一定偏导数连续

一个形象的角度理解：多元函数可微、可导、连续的关系 - 知乎 (zhihu.com)

连续：在定义范围内曲面上没有窟窿、断崖（但可以有尖点，有折痕）

(偏)导函数存在，即可导：曲面和某个切面相交的那条切线是光滑的（但是偏导函数可以在这点不连续，即极限存在但无定义)

可微：曲面是光滑的(想象一个穹顶)

偏导数、方向导数、梯度

参考阅读：

直观理解梯度，以及偏导数、方向导数和法向量等 - shine-lee - 博客园 (cnblogs.com)

导数，偏导数，方向导数，梯度的理解—-微积分数学基础SUSAN的博客

通俗理解方向导数与梯度 - 知乎 (zhihu.com)

多元函数的偏导数、方向导数、梯度以及微分之间的关系思考 - 知乎 (zhihu.com)

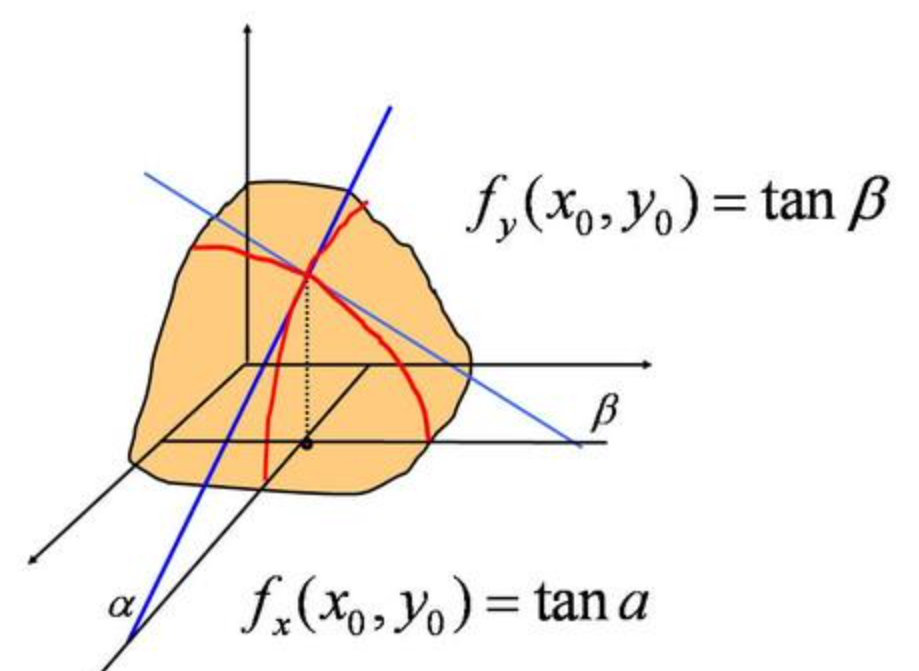
🔴 $\textcolor{red}{偏导数}$

对于多元函数，求导数其实也是要求一个切线的斜率，但是由于曲面上的一个点的切线有无数条，那么取那条切线的斜率？引入： 偏导数。

偏导数：可以理解成多元函数“退化”成一元函数时的导数 ；“退化”：固定其他变量的值，只保留一个变量，依次保留每个变量，则$N$元函数有$N$个偏导数。

几何意义：也是切线斜率，由于曲面上一点的切线有无数条（所有切线组成一个切面），偏导数选取的是垂直于各坐标轴的几条特殊切线的斜率。
物理意义：表示函数沿着某个坐标轴方向上的变化率

以二元函数$z=f(x,y)$为例，求$(x_0,y_0,z_0)$的偏导数：

对$x$的偏导数：过点$(x_0,y_0,z_0)$且垂直于$y$轴的曲线（相当于固定$y$值），在该点切线的斜率
对$y$的偏导数：过点$(x_0,y_0,z_0)$且垂直于$x$轴的曲线（相当于固定$x$值），在该点切线的斜率

🔴 $\textcolor{red}{方向导数}$

偏导数计算的是垂直于各坐标轴的几条特殊切线的斜率，某点的切线沿着不同方向有无数条 👉想求某点沿着任意方向的切线斜率？引入：方向导数（补充：既然切线都分布在一个平面上，并且每一条切线都代表着函数朝着某一方向的变化率，那么在这个平面上就必定会存在唯一的一条切线的方向导数最大。（梯度为0的情况除外）

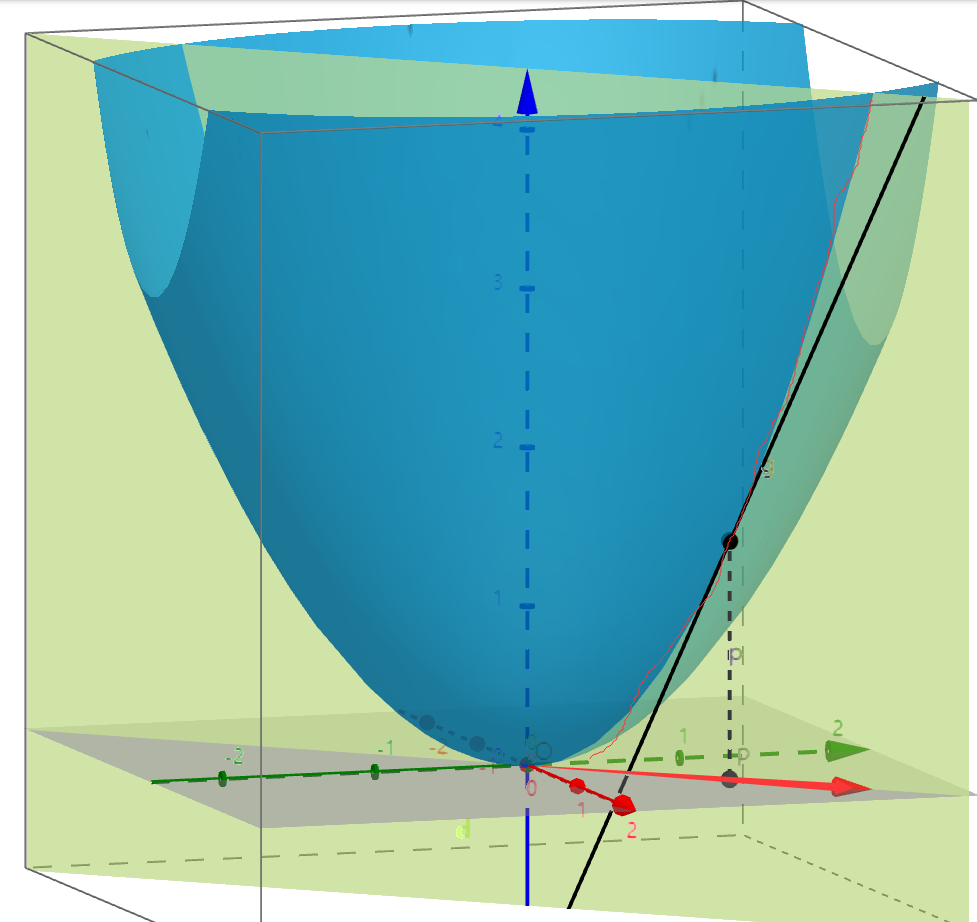
以二元函数$z=f(x,y)$为例，求$(x_0,y_0,z_0)$的某方向导数：（下图动态演示地址）

$x$轴和$y$轴决定的平面上选择某一个方向向量（图中斜着的红色箭头），该方向所在的这个黄色平面与蓝色曲面相交决定了一条过$(x_0,y_0,z_0)$的曲线（隐隐约约的红色细线描出来的部分），点在该曲线上的这条黑色切线斜率即为方向导数

设一个方向向量为$\overrightarrow{\mathrm{u}}=(\cos \alpha, \sin \alpha)$ （$\alpha$和$\beta$分别为该方向向量与$x$轴和$y$轴的夹角），则方向导数定义如下，它是个标量： $\mathrm{D}_{\mathrm{u}} \mathrm{f}(\mathrm{x}, \mathrm{y})=\mathrm{f}_{\mathrm{x}}(\mathrm{x}, \mathrm{y}) \cos \alpha+\mathrm{f}_{\mathrm{y}}(\mathrm{x}, \mathrm{y}) \sin \alpha$ 进一步地，设偏导向量$\overrightarrow{\mathrm{A}}=\left(\mathrm{f}_{\mathrm{x}}(\mathrm{x}, \mathrm{y}), \mathrm{f}_{\mathrm{y}}(\mathrm{x}, \mathrm{y})\right)$，则上述方向导数可以改写为： $\mathrm{D}_{\mathrm{u}} \mathrm{f}(\mathrm{x}, \mathrm{y})=\overrightarrow{\mathrm{A}} * \overrightarrow{\mathrm{u}}=|\overrightarrow{\mathrm{A}}| *|\overrightarrow{\mathrm{u}}| * \cos (\theta)$ $ \theta$ 是偏导向量和方向向量之间的夹角。当$\theta=0$即二者同向时，方向导数$D_{u} f(x, y)$取得正最大值。反向时，则负最大值。

🔴 $\textcolor{red}{梯度}$

梯度：是一个矢量，函数在某点无数个变化方向中 变化最快的 那个方向

即：偏导数构成的向量；由此：方向导数 = 梯度 * 方向向量

函数只要每一个变量都沿着关于这个变量的偏导所指定的方向来变化，函数的整体变化就能达到最快（变化的绝对值最大）

梯度的几何意义：

当前位置的梯度方向，为函数在该位置处方向导数最大的方向，也是函数值上升最快的方向，反方向为下降最快的方向；
当前位置的梯度长度（模），为最大方向导数的值
梯度（下降）的方向与等高线的切线方向垂直

以二元函数$z=f(x,y)$为例，其方向导数定义如下：

$\nabla f\left(x_{0}, y_{0}\right)=\left.\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\right|_{\left(x_{0}, y_{0}\right)}$

微积分基础

参考视频：3-定积分_哔哩哔哩_bilibili

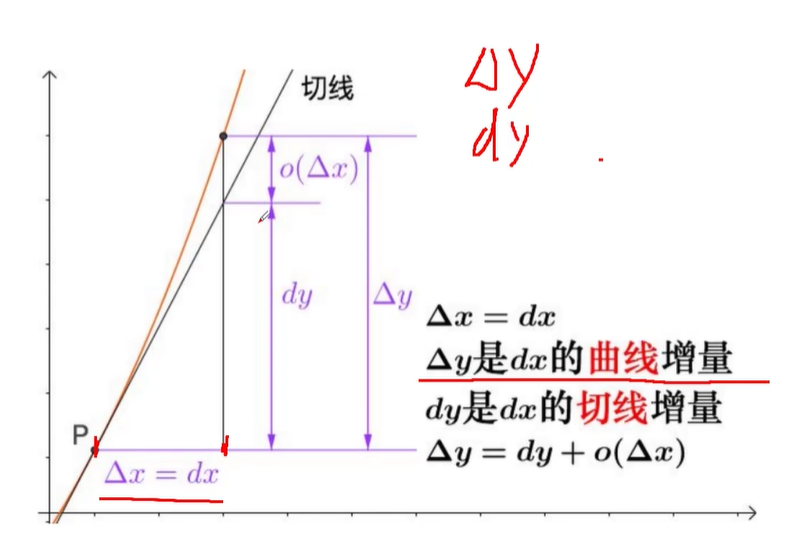
🔴 $\textcolor{red}{区分\Delta y和dy}$

定积分

🔴 $\textcolor{red}{定义}$

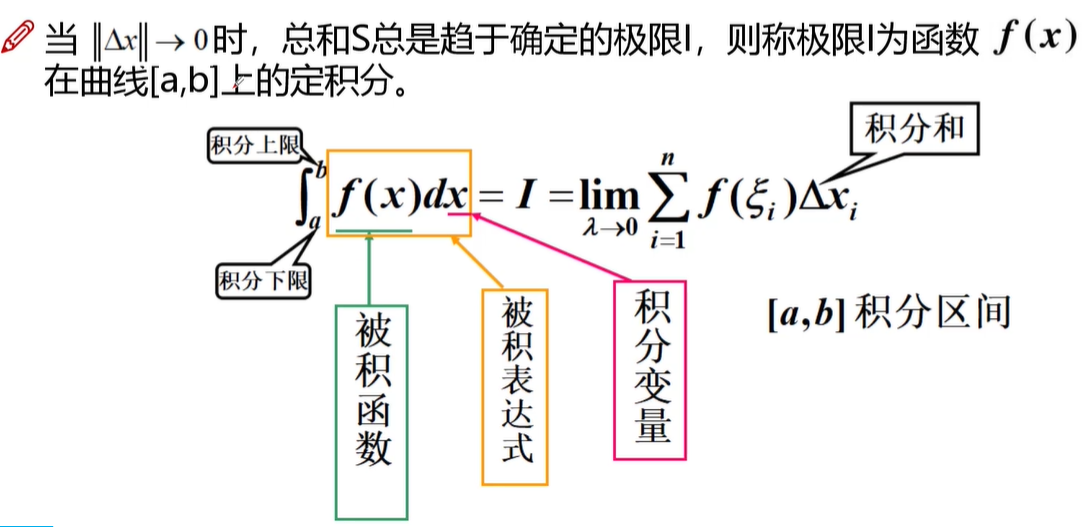
🔴 $\textcolor{red}{积分上限函数}$

函数$f(x)$在区间$[a,b]$上连续，对于定积分$\int_{a}^{x} f(x) d x$每一个取值$x$都有一个对应的定积分值，记作$\Phi(x)= \int_{a}^{x} f(t) dt$

若函数$f(x)$在区间$[a,b]$上连续，则积分上限函数就是$f(x)$在$[a,b]$上的原函数

两大积分中值定理

🔴 $\textcolor{red}{第一中值定理}$

如果函数$f(x)$在闭区间$[a,b]$上连续，则在积分区间$[a,b]$上，至少存在一个点$\xi$，使$\int_{a}^{b} f(x) d x=f(\xi)(b-a) . \quad(a \leq \xi \leq b)$

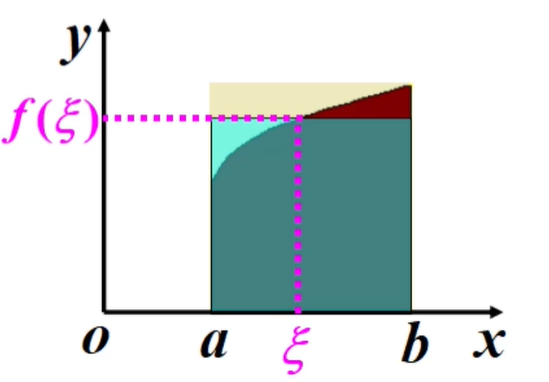
🔴 $\textcolor{red}{第二中值定理}$

三大微分中值定理

牛顿-莱布尼兹公式

🔴 $\textcolor{red}{定义}$

如果$F(x)$是连续函数$f(x)$在区间$[a,b]$上的一个原函数，则$\int_{a}^{b} f(x) d x=F(a)-F(b)$。

即：一个连续函数在区间$[a,b]$上的定积分等于它的任意一个原函数在区间$[a,b]$上的增量

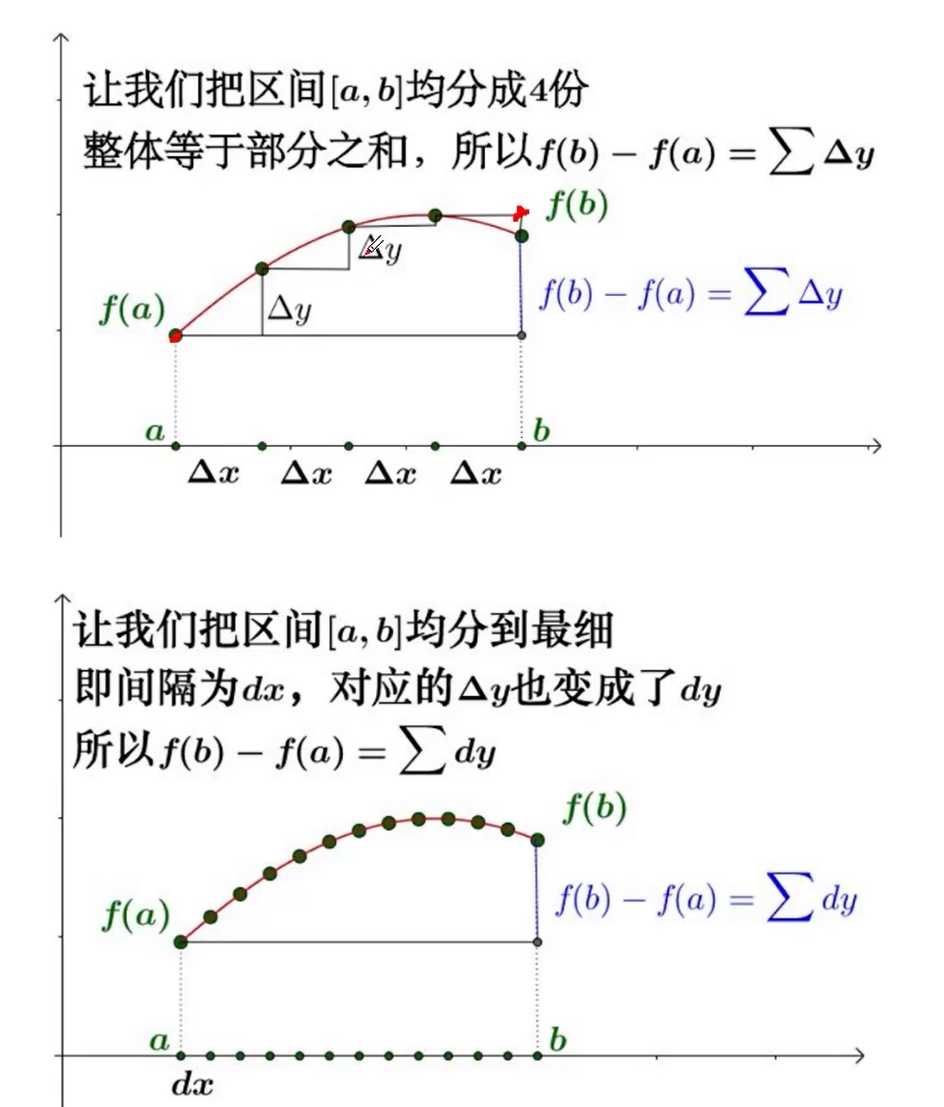
🔴 $\textcolor{red}{几何解释}$

可得：$f(b)-f(a)=\sum dy$，由于$dy=f’(x)dx$，$f(b)-f(a)=\sum f’(x)dx= \int_{a}^{b}f’(x)dx $

泰勒公式

用简单的熟悉的多项式来近似代替复杂的函数

🔴 $\textcolor{red}{泰勒多项式}$

$f(x)$在$x_0$关于$(x-x_0)$的n阶泰勒多项式：

$\begin{array}{l} P_{n}(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+ \cdots \quad+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n} \end{array}$

🔴 $\textcolor{red}{麦克劳林公式}$

令$x_0=0$：

$\begin{aligned} f(x)=& f(0)+f^{\prime}(0) x+\frac{f^{\prime \prime}(0)}{2 !} x^{2}+\cdots+\frac{f^{(n)}(0)}{n !} x^{n}+\frac{f^{(n+1)}(\theta x)}{(n+1) !} x^{n+1}(0<\theta<1) \end{aligned}$

🔴 $\textcolor{red}{泰勒多项式中阶数的作用}$

阶数越高，增长速度越快；越高次项在越偏右侧影响越大
对于一个复杂函数，低阶项能更好地描述当前点附近，对于之后的走势就越来越依靠高阶项

傅里叶级数

拉格朗日乘子法

寻找变量受一个或多个条件限制的多元函数的极值

参考阅读：

如何理解拉格朗日乘子法？ - 知乎 (zhihu.com)

【线性分类器】（四）万字长文解释拉格朗日乘子与支持向量机_二进制人工智能的博客-CSDN博客

【数学】拉格朗日对偶，从0到完全理解_frostime的博客（←这篇博客写得超级超级好！）

高数中的拉格朗日乘子

条件极值：对函数的自变量还有附加条件的极值

求解条件极值：拉格朗日乘子法

例如对于一个二元函数函数：$z=f(x,y)$在条件$\varphi(x, y)=0$下的极值，构造拉格朗日函数$F(x,y)=f(x,y)+\lambda \varphi(x, y)$，其中$\lambda$为拉格朗日乘数，构造下列函数求得极值点坐标：

$\left\{\begin{array}{c} f_{x}(x, y)+\lambda \varphi_{x}(x, y)=0 \\ f_{y}(x, y)+\lambda \varphi_{y}(x, y)=0 \\ \varphi(x, y)=0 \end{array}\right.$

凸优化

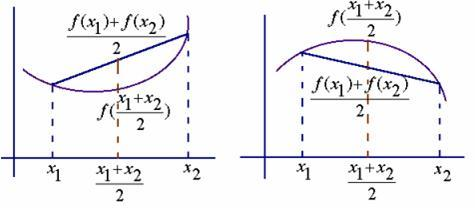
凸函数、凹函数、仿射函数

左图是凸函数，右图是凹函数；

凹凸可以转化：对于凹函数f，− f即为凸函数。

凸函数：

$\forall \mathrm{x}, \mathrm{y} \in \operatorname{dom} \mathrm{f}, \quad \forall \theta \in[0,1] \\ \mathrm{f}(\theta \mathrm{x}+(1-\theta) \mathrm{y}) \leqslant \theta \mathrm{f}(\mathrm{x})+(1-\theta) \mathrm{f}(\mathrm{y})$

凹函数

$\forall \mathrm{x}, \mathrm{y} \in \operatorname{dom} \mathrm{f}, \quad \forall \theta \in[0,1] \\ \mathrm{f}(\theta \mathrm{x}+(1-\theta) \mathrm{y}) \geqslant \theta \mathrm{f}(\mathrm{x})+(1-\theta) \mathrm{f}(\mathrm{y})$

仿射函数既凹又凸：

$\mathrm{f}(\theta \mathrm{x}+(1-\theta) \mathrm{y}) = \theta \mathrm{f}(\mathrm{x})+(1-\theta) \mathrm{f}(\mathrm{y})$ $\overrightarrow{\mathrm{x}} \rightarrow \mathrm{A} \overrightarrow{\mathrm{x}}+\overrightarrow{\mathrm{b}} \quad被称为\quad \mathbb{R}^{\mathrm{n}} \rightarrow \mathbb{R}^{\mathrm{m}} 的仿射变换，这一过程被称为仿射函数。 \\ f(x)=A x+b, x \in \mathbb{R}^{n} \\ 比如最简单的: \mathrm{a}_{1} \mathrm{x}_{1}+\mathrm{a}_{2} \mathrm{x}_{2}+\cdots+\mathrm{a}_{\mathrm{n}} \mathrm{x}_{\mathrm{n}}+\mathrm{b} 就是一个仿射函数。$

凸优化

凸优化问题就是满足特定条件的优化问题，任意位置的局部最优解同时也是全局最优解

凸优化问题的基本形式描述：

$\begin{array}{ll} \min _{\mathrm{x} \in \mathbb{R}^{\mathrm{n}}} \mathrm{f}(\mathrm{x}) \\ \text { s.t } & \mathrm{c}_{\mathrm{i}}(\mathrm{x}) \leqslant 0, \mathrm{i} \in[1, \mathrm{k}] \\ & \mathrm{h}_{\mathrm{j}}(\mathrm{x})=0, \mathrm{j} \in[1,l] \end{array}$

要求满足：

$f(x)$ 是凸函数
$c_i(x)$是凸函数
$h_j(x)$是仿射函数

从广义拉格朗日函数到拉格朗日对偶函数

原问题

针对上述原问题，首先约定：

不假定$f(x)$的凹凸性，可以非凹非凸
原问题的定义域：$\mathrm{D}=(\operatorname{dom} \mathrm{f}) \cap\left(\bigcap_{\mathrm{i}=1}^{\mathrm{k}} \mathrm{c}_{\mathrm{i}}\right) \cap\left(\bigcap_{\mathrm{i}=1}^{\mathrm{l}} \mathrm{h}_{\mathrm{i}}\right) \neq \empty$
最终求出的最优结果表示：$p^ * $

对于该原问题，不太好解，难点在于：

约束条件多：$k+l$ 个约束
$f(x)$凹凸性不明确，意味着无法运用凸优化的方法

因此，考虑采用拉格朗日对偶的方式求解，优点在于：

对偶：实质相同，但同不同角度提出不同提法的一对问题

只有一个约束
拉格朗日对偶问题一定是凹的

将非凸目标函数的极小化转换成凹目标函数的极大化，局部极值点便是全局极值点

广义拉格朗日函数

$\begin{array}{l} \mathcal{L}: \mathbb{R}^{\mathrm{n}} \times \mathbb{R}^{\mathrm{k}} \times \mathbb{R}^{l} \rightarrow \mathrm{R} \\ \mathcal{L}(\mathrm{x}, \lambda, \mu)=\mathrm{f}(\mathrm{x})+\sum_{\mathrm{i}=1}^{\mathrm{k}} \lambda_{\mathrm{i}} \mathrm{c}_{\mathrm{i}}(\mathrm{x})+\sum_{\mathrm{j}=1}^{l} \mu_{\mathrm{j}} \mathrm{h}_{\mathrm{j}}(\mathrm{x}) \\ \overrightarrow{\mathrm{x}} \in \mathbb{R}^{\mathrm{n}}, \vec{\lambda} \in \mathbb{R}^{\mathrm{k}}, \vec{\mu} \in \mathbb{R}^{l} \end{array}$

拉格朗日对偶函数

🔸 不管原函数$f$的凹凸性，它的对偶函数$g$一定是一个凹函数

相关证明详见：【数学】拉格朗日对偶，从0到完全理解_frostime的博客

$\begin{aligned} \mathrm{g}(\lambda, \mu) &=\inf _{\mathrm{x} \in \mathrm{D}} \mathcal{L}(\mathrm{x}, \lambda, \mu) \\ &=\inf _{\mathrm{x} \in \mathrm{D}}\left(\mathrm{f}(\mathrm{x})+\sum_{\mathrm{i}=1}^{\mathrm{k}} \lambda_{\mathrm{i}} \mathrm{c}_{\mathrm{i}}(\mathrm{x})+\sum_{\mathrm{j}=1}^{l} \mu_{\mathrm{j}} \mathrm{h}_{\mathrm{j}}(\mathrm{x})\right) \\ \lambda \geqslant 0 \end{aligned}$

inf：下确界，和min类似，但细节部分略不同

这个对偶函数能给出原问题最优解的下确界：

相关证明详见：【数学】拉格朗日对偶，从0到完全理解_frostime的博客

$\forall \lambda \geqslant 0 \Rightarrow \mathrm{g}(\lambda, \mu) \leqslant \mathrm{p}^{*}$

🔸 也就是说，无论如何，$p^$ 都 *不会小于 $max g(\lambda,\mu)$

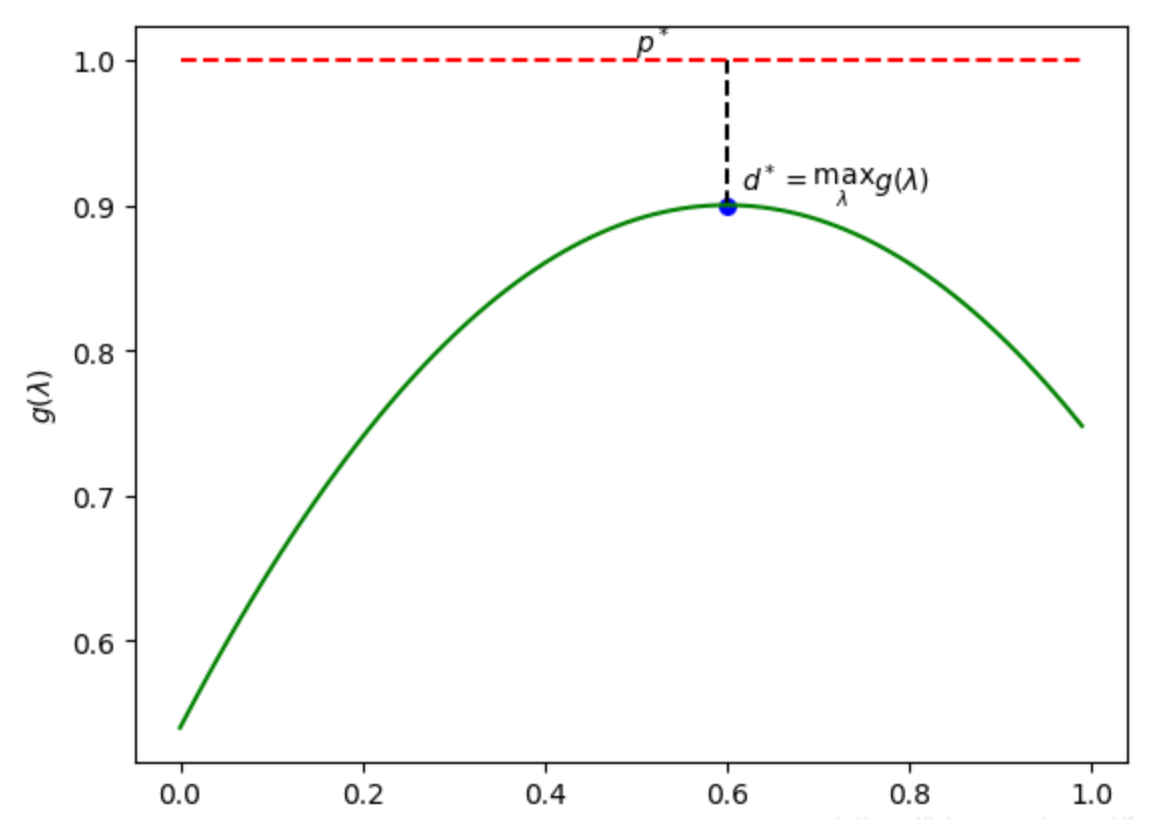
最初的目的是找到原问题的最优解 $p^ * $，但有时候该解并不一起能解出来，因此希望可以给出一个尽可能逼近

$p^ * $的值：$\max \operatorname{g}(\lambda, \mu)(\text { s.t } \lambda \geqslant 0)$

总结：原问题vs对偶问题

🔸 原问题（Primal Problem），结果记为$p^ * $

🔸 拉格朗日对偶问题（Lagrange Dual Problem），结果记为$d^*$

$\begin{array}{ll} 转换为\mathcal{L}(\mathrm{x}, \lambda, \mu)=\mathrm{f}(\mathrm{x})+\sum_{\mathrm{i}=1}^{\mathrm{k}} \lambda_{\mathrm{i}} \mathrm{c}_{\mathrm{i}}(\mathrm{x})+\sum_{\mathrm{j}=1}^{l} \mu_{\mathrm{j}} \mathrm{h}_{\mathrm{j}}(\mathrm{x})\\ 求\max _{\lambda, \mu} g(\lambda, \mu)=\max _{\lambda, \mu} \inf _{\mathrm{x} \in \mathrm{D}} \mathcal{L}(\mathrm{x}, \lambda, \mu) \\ s.t \quad \lambda_{\mathrm{i}} \geqslant 0, \mathrm{i}=1,2, \ldots, \mathrm{k} \end{array}$

希望求p* ，但不好求，因此求d*

因为 d* ≤ p* $，至少说明能求得 $ p*的下界，如果在非常理想，或者说，满足具体特定条件时，等式就成立了

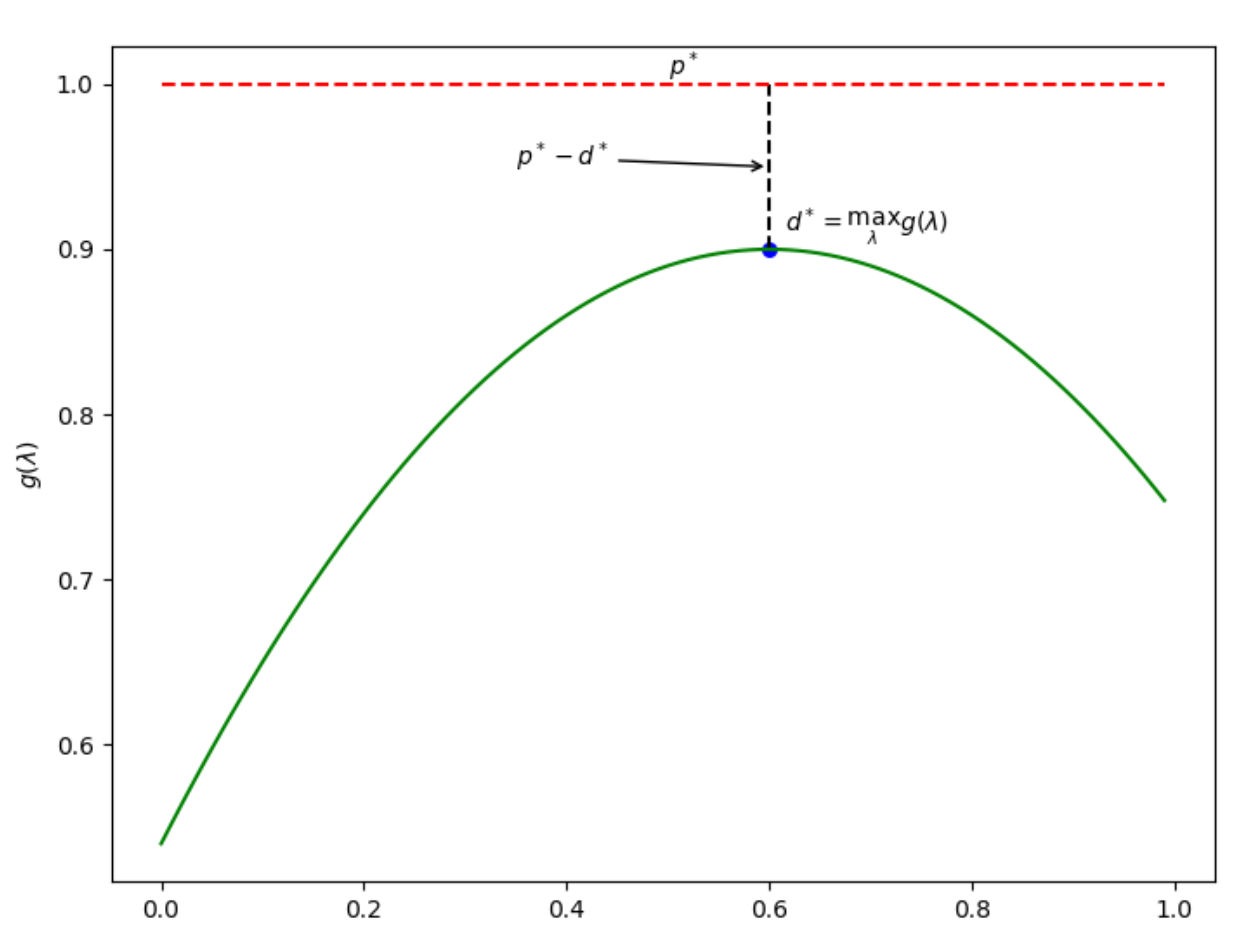
强、弱对偶

弱对偶—— d* ≤ p* ：

最优对偶间隙（Optimal Duality Gap）：p* -d*

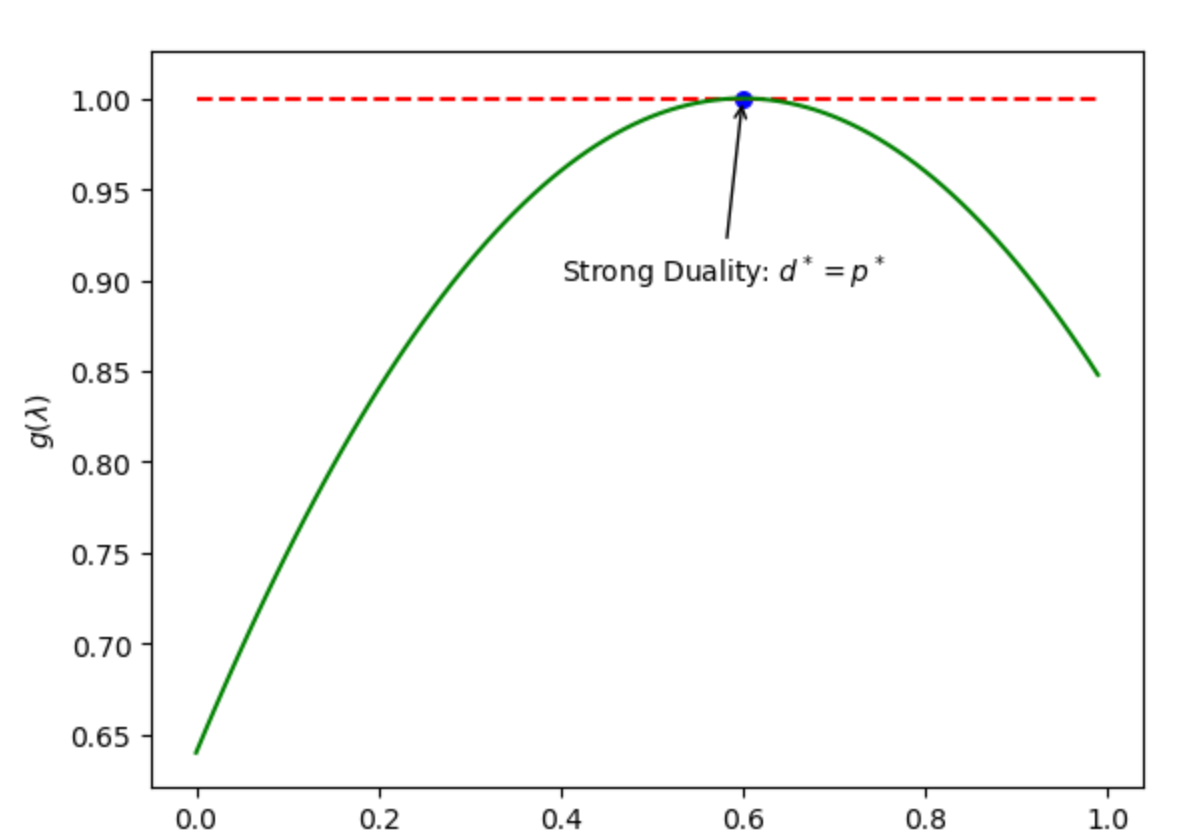
强对偶——d*= p*：

如果满足强对偶，只要求出了d*，就相当于求出了p*
必须满足一定的条件，强对偶才可能成立（使满足强对偶的条件有多种）

关于强对偶和最优的条件

Convex+Slater

满足强对偶的一个充分条件

🔴 即：原问题是凸优化且满足 Slater条件，则一定满足强对偶

Slater条件：

$\begin{array}{l} \exists \mathrm{x} \in \mathrm{D} \\ \mathrm{c}_{\mathrm{i}}(\mathrm{x})<0, \mathrm{i} \in[1, \mathrm{k}] \\ \mathrm{Ax}=\mathrm{b} \end{array}$

KKT条件

非凸问题下的KKT

暂略…

凸问题下的KKT

凸问题下，满足 KKT 条件的点一定是原问题和对偶问题的最优解；

KKT 条件成了强对偶和最优解的充要条件

🔴也就是说：

若原问题是凸（Convex）的
$\mathcal{L}(\mathrm{x}, \lambda, \mu)=\mathrm{f}(\mathrm{x})+\sum_{\mathrm{i}=1}^{\mathrm{k}} \lambda_{\mathrm{i}} \mathrm{c}_{\mathrm{i}}(\mathrm{x})+\sum_{\mathrm{j}=1}^{l} \mu_{\mathrm{j}} \mathrm{h}_{\mathrm{j}}(\mathrm{x})$
$\exists \hat{\mathrm{x}}, \hat{\lambda}, \hat{\mu}$，满足：
$\begin{array}{lr} (1)\quad\mathrm{c}_{\mathrm{i}}(\hat{\mathrm{x}}) \leqslant 0 & \mathrm{i}=1, \ldots, \mathrm{k} \\ (2)\quad\mathrm{h}_{\mathrm{i}}(\hat{\mathrm{x}})=0 & \mathrm{i}=1, \ldots, l \\ (3)\quad\hat{\lambda}_{\mathrm{i}} \geqslant 0 & \mathrm{i}=1, \ldots, \mathrm{k} \\ (4)\quad\hat{\lambda}_{\mathrm{i}} \mathrm{c}_{\mathrm{i}}(\hat{\mathrm{x}})=0 & \mathrm{i}=1, \ldots, \mathrm{k} \\ (5)\quad\nabla \mathrm{f}(\hat{\mathrm{x}})+\sum_{\mathrm{i}=1}^{\mathrm{k}} \hat{\lambda}_{\mathrm{i}} \nabla \mathrm{c}_{\mathrm{i}}(\hat{\mathrm{x}})+\sum_{\mathrm{i}=1}^{l} \hat{\mu}_{\mathrm{i}} \nabla \mathrm{h}_{\mathrm{i}}(\hat{\mathrm{x}})=0 & \end{array}$

(1)（2）：满足原问题的等式和不等式约束（原问题可行）

(3)：满足非负性（弱对偶的必要条件）（对偶问题可行）

(4)：互补松弛条件，防止出现$\mathrm{c}_{\mathrm{i}}(\hat{\mathrm{x}})>0$

(5)：$x$* 是最优点，理所当然的，原问题 $\mathcal{L}$ 关于 $x$* 的导数必须等于 0。
那么，$\hat{\mathrm{x}}, \hat{\lambda}, \hat{\mu}$都是原问题和对偶问题的最优解，且最优对偶间隙为0，满足强对偶性。

矩阵分析中的拉格朗日乘子

含有一个等式约束的最优化

实函数$f(w)$是参数向量$w$ 的函数，约束条件：$w^Tx=b$，其中$x$是已知向量，$b$是常数，令$h(w)=w^Tx-b=0$，最小化问题可以描述为

$minf(w) \quad s.t.\quad h(w)=0$

引入拉格朗日乘子，将上述约束最小化问题转化为无约束问题，定义新函数，利用偏导求参即可：

$\mathrm{L}(\mathrm{w}, \lambda)=\mathrm{f}(\mathrm{w})+\lambda \mathrm{h}(\mathrm{w})$

含有多个等式约束的最优化

实函数$f(w)$是参数向量$w$的二次函数，约束条件：$w^Tx_k=b_k,k=1,2,\dots K$，其中$x$是已知向量，$b_k$是常数，令$h_k(w)=w^Tx_k-b_k=0$，最小化问题描述为：

$minf(w)\quad s.t.\quad h_k(w)=0,k=1,2,\dots K$

将上述最小化问题转化为无约束问题，定义一个新的实函数：

$\mathrm{L}(\mathrm{w}, \lambda)=\mathrm{f}(\mathrm{w})+\sum_{\mathrm{k}=1}^{\mathrm{K}} \lambda_{\mathrm{k}} \mathrm{h}_{\mathrm{k}}(\mathrm{w})$

拉格朗日对偶问题

函数$f(x)=max\{x_1,x_2,\dots,x_n\}$是$R^n$上的凸函数

函数$f(x)=min\{x_1,x_2,\dots,x_n\}$是$R^n$上的凹函数

约束优化的原始问题模型：

$\min _{x} f_{0}(x)\\ s.t.\quad \mathrm{f}_{\mathrm{i}}(\mathrm{x}) \leq 0, \mathrm{i}=1, \ldots \mathrm{m} \\ \quad\quad \mathrm{h}_{\mathrm{i}}(\mathrm{x})=0, \mathrm{i}=1, \ldots \mathrm{q}$

利用拉格朗日乘子法可以松弛为无约束优化问题（对偶问题）：

$\min \mathrm{L}(\mathrm{x}, \lambda, \mathrm{v})=\mathrm{f}_{0}(\mathrm{x})+\sum_{\mathrm{i}=1}^{\mathrm{m}} \lambda_{\mathrm{i}} \mathrm{f}_{\mathrm{i}}(\mathrm{x})+\sum_{\mathrm{i}=1}^{\mathrm{q}} \mathrm{v}_{\mathrm{i}} \mathrm{h}_{\mathrm{i}}(\mathrm{x})$

LiaN

【SE】高等数学