朴素贝叶斯
参考文献链接:
「一个模型」教你搞定贝叶斯和全概率公式_哔哩哔哩_bilibili
基础知识
先验概率:$P(A)$:在不考虑任何情况下,事件A发生的概率
联合概率:$P(AB)$:两个(或更多)不同事件同时发生的概率,即两个(或更多)同时发生的事件
条件概率:$P(A|B)$:在事件B已发生的情况下,事件A发生的概率
若只有事件A和B,因为:$\mathrm{P}(\mathrm{AB})=\mathrm{P}(\mathrm{A} \mid \mathrm{B}) \mathrm{P}(\mathrm{B})=\mathrm{P}(\mathrm{B} \mid \mathrm{A}) \mathrm{P}(\mathrm{A})$,因此,得到贝叶斯公式:
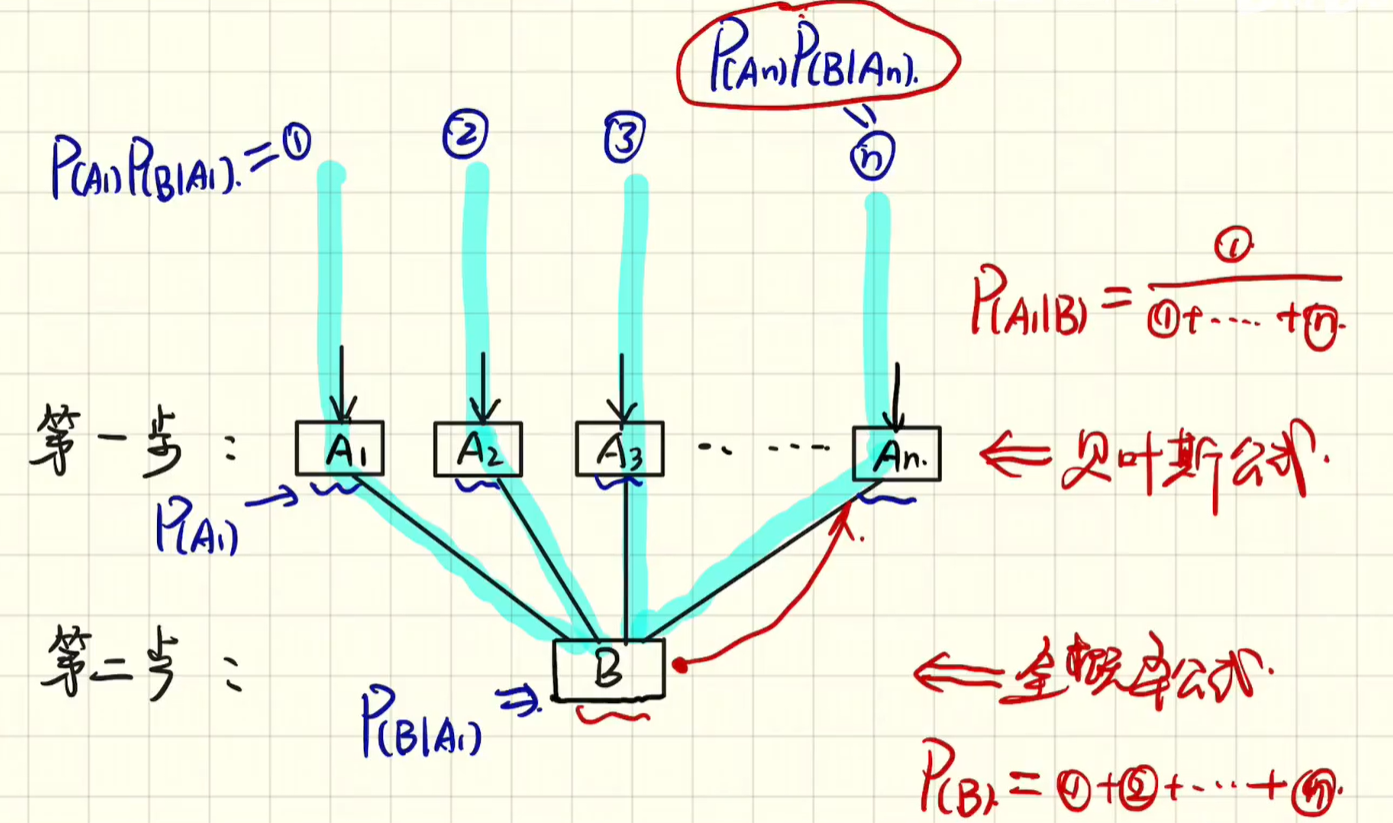
全概率公式
贝叶斯公式
对于上式,分母是一个固定值,只需要比较分子大小即可。把$P(A_i)$称为先验概率,$P(A_i|B)$称为后验概率,$P(B|A_i)$称为似然函数:先验 * 似然 = 后验
生成模型 vs 判别模型
生成模型
- 由数据学得联合概率分布,求出条件概率分布P(Y|X)的预测模型;
判别模型
- 由数据学得决策函数或条件概率分布作为预测模型
最大似然 vs 奥卡姆剃刀
最大似然
- 最符合观测数据的最有优势
- 根据观测的数据找出哪些是最有优势的,比如投一个硬币就投一次,观测到的为正,那么根据最大似然估计可以预测下一次投正的概率为1,这只是投一次的情况,如果投很多次,那也能预测出投正的概率大概为0.5,简单来说,最大似然估计原理就是根据投掷结果来预测以后
奥卡姆剃刀
- 认为先验概率较大的具有较大的优势,追寻的是实际中什么东西最常见什么东西就是越好的。
朴素贝叶斯
🔴 概括:朴素贝叶斯是生成模型,基于很强的条件独立假设(在已知分类c的条件下,各个特征变量取值是相互独立的),根据已有样本学习出先验概率$p(c)$,和 条件概率$p(\boldsymbol x|c$),计算出联合概率$p(\boldsymbol x,c)$,再利用贝叶斯定理求出条件概率$p(c|\boldsymbol x)$。
🔴 为什么说“朴素”?:因为朴素贝叶斯分类假定所有的特征在数据集中的作用是同样重要和独立的,而这个假设在现实世界中是很不真实的(确切的说,应该是很“天真”,英文:“naive bayes”),毕竟现实世界中,特征之间存在一定的依赖关系
特征条件独立假设 在分类问题中,常常需要把一个事物分到某个类别中。已知一个事物有许多属性$\boldsymbol x=(x_1,x_2,\dots,x_n)$,求其属于类别$c$的概率
朴素贝叶斯的假设函数:
分母$p(\boldsymbol{x})$是常数,分子中,由于假设特征独立分布(各个条件之间互不影响),所以$p(\boldsymbol{x} \mid c) =\prod_{i=1}^{n} p\left(x_{i} \mid c\right)$,因此有:
朴素贝叶斯分类器的训练过程就是 基于训练集来估计 类先验概率$p(c)$ 的每个特征的条件概率$p(x_i|c)$
根据极大似然估计
总结:朴素贝叶斯就是在统计数据的基础上,依据条件概率公式,计算当前特征的样本属于各个分类的概率,哪个最大,就认为此待分类项属于哪个类别。
对数据的处理:
离散数据:取值类别有限或可数的特征,计算概率十分简单就是数数,计算在某一条件下某一个特征出现的概率即为求解条件概率。
连续数据:取值连续的特征,朴素贝叶斯在处理时默认各个连续特征都服从正态分布,根据训练数据计算每个特征的均值和方差,做测试集预测时,带入正态分布的概率密度公直接计算概率密度值作为该特征出现的概率。如果最终的分类数有N种,那么对每个连续特征而言就有N套(均值,方差)分别对应不同的分类类别。
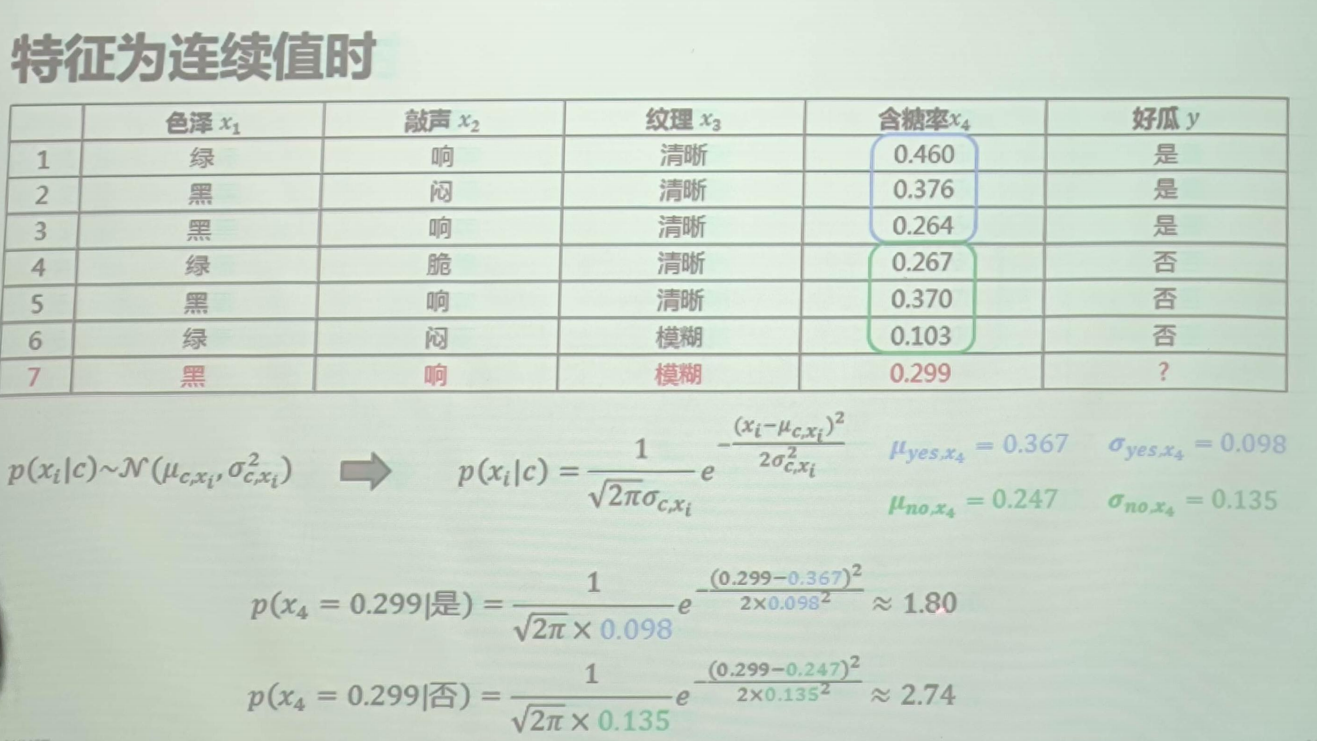
优缺点
优点
- 对小规模数据表现良好、适合多分类任务、增量式训练
缺点
- 对数据数据的表达形式敏感(离散、连续、极大极小)
应用实例
例1:瓜的预测
| 色泽$x_1$ | 敲声$x_2$ | 纹理$x_3$ | 好瓜$y$ | |
|---|---|---|---|---|
| 1 | 绿 | 响 | 清晰 | 是 |
| 2 | 黑 | 闷 | 清晰 | 是 |
| 3 | 黑 | 响 | 模糊 | 是 |
| 4 | 绿 | 脆 | 清晰 | 否 |
| 5 | 黑 | 响 | 清晰 | 否 |
| 6 | 绿 | 闷 | 模糊 | 否 |
| 7 | 黑 | 响 | 模糊 | ? |
根据上式,有:$p(是|黑,响,模糊)=p(是)\times [p(x_1=黑|是)\times p(x_2=响|是)\times p(x_3=模糊|是)]$
计算得到$3/6\times 2/3\times 2/3\times 1/3=4/54$
拉普拉斯平滑
如果将上表中第3条数据的纹理属性值改为“清晰”,那么计算的结果会是0,显然有问题。因此,为了解决零概率问题,需要做加法平滑,也就是拉普拉斯平滑。
假定训练样本很大时,每个分量$x$的计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题。
在分子、分母上各加一个数值,下式中,$N$是训练集中的类别总数
下式中,$N_i$是 第$i$个特征可能的取值数
例2:文本分类
文本分类的多项式模型:重复词语视为出现多次
| 文档 | 文本 | 标签$y$ |
|---|---|---|
| 1 | Chinese,Beijing,Chinese | C |
| 2 | Chinese,Chinese,Shanghai | C |
| 3 | Chinese,Macao | C |
| 4 | Tokyo,Japan,Chinese | J |
| 5 | Chinese,Chinese,Chinese,Tokyo,Japan | ? |
构建词向量
| $w_1$ | $w_2$ | $w_3$ | $w_4$ | $w_5$ | $w_6$ |
|---|---|---|---|---|---|
| Beijing | Chinese | Japan | Macao | Shanghai | Tokyo |
对训练集中 词语的出现次数 进行统计
| N(doc) | $w_1$ | $w_2$ | $w_3$ | $w_4$ | $w_5$ | $w_6$ | $y$ |
|---|---|---|---|---|---|---|---|
| 3 | 1 | 5 | 0 | 1 | 1 | 0 | C |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | J |
根据公式计算条件概率:$\tilde{p}\left(w_{i} \mid c\right)=\frac{\left|D_{c, w_{i}}\right|+1}{\left|D_{c}\right|+N}$,($N=6$:因为$w$有6种取值),得到下表:
| $p(doc)$ | $w_1$ | $w_2$ | $w_3$ | $w_4$ | $w_5$ | $w_6$ | |
|---|---|---|---|---|---|---|---|
| $p(w_i\vert y=C)$ | $\frac{3}{4}$ | $\frac{2}{14}$ | $\frac{6}{14}$ | $\frac{1}{14}$ | $\frac{2}{14}$ | $\frac{2}{14}$ | $\frac{1}{14}$ |
| $p(w_i\vert y=J)$ | $\frac{1}{4}$ | $\frac{1}{9}$ | $\frac{2}{9}$ | $\frac{2}{9}$ | $\frac{1}{9}$ | $\frac{1}{9}$ | $\frac{2}{9}$ |
因此,对文档5进行预测,比较概率大小,可得属于C类:
TF-IDF
在看朴素贝叶斯的文本分类的例子时,无意间看到这个算法,之前听说过,但没仔细看过,nlp相关的,就顺便学一下,虽然这个和朴素贝叶斯没啥关系的样子
基本介绍
TF-IDF(term frequency–inverse document frequency,词频-逆向文件频率)是一种用于信息检索(information retrieval)与文本挖掘(text mining)的常用加权技术。
用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。
🔴 TF-IDF的主要思想:如果某个单词在一篇文章中出现的频率高(IF),并且在其他文章中很少出现(IDF),则认为此词或者短语具有很好的类别区分能力,适合用来分类。
TF:词频(Term Frequency)
词条在文本中出现的频率,一般会被归一化(词频 / 文字总词数),以防止它偏向长的文件
其中,$n_{i,j}$表示词条$t_i$在文档 $d_j$ 中出现的次数,$TF_{i,j}$ 表示 词条$t_i$在文档$d_j$ 中出现的频率。
IDF:逆文件频率(Inverse Document Frequency)
所有统计的文章中,一些词只是在其中很少几篇文章中出现,那么这样的词对文章的主题的作用很大,这些词的权重应该设计的较大。IDF就是在完成这样的工作。
IDF表示关键词的普遍程度。如果包含词条 i 的文档越少, IDF越大,则说明该词条具有很好的类别区分能力。某一特定词语的IDF,可以由总文档数目除以包含该词语的文件的数目,再将得到的商取对数得到
其中,$|D|$总文档数目,$\left|j: t_{i} \in d_{j}\right|$ 包含词条$t_i$的文档数目,加1 防止包含词条$t_i$的 文档数目为0导致运算错误。
TF-IDF
某一特定文件内的高词语频率,以及该词语在整个文件集合中的低文件频率,可以产生出高权重的TF-IDF。因此,TF-IDF倾向于过滤掉常见的词语,保留重要的词语,表达为
TF-IDF算法非常容易理解,很容易实现,但是其简单结构并没有考虑词语的语义信息,无法处理一词多义与一义多词的情况