【机器学习】Logistic回归模型

逻辑回归（Logistic Regression）

参考文献链接：

【机器学习】逻辑回归（非常详细） - 知乎 (zhihu.com)

逻辑回归（Logistic Regression）（一） - 知乎 (zhihu.com)

基本介绍

• Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。

• 本质：假设数据服从这个分布（假设函数），然后使用极大似然估计做参数的估计：$\theta$。

假设函数（Hypothesis function)

Sigmoid函数

也称逻辑函数（Logistic function）：

$$g(z)=\frac{1}{1+e^{-z}}$$

该函数的曲线如下，取值范围$[0,1]$：将实数$z$映射到这个范围内：

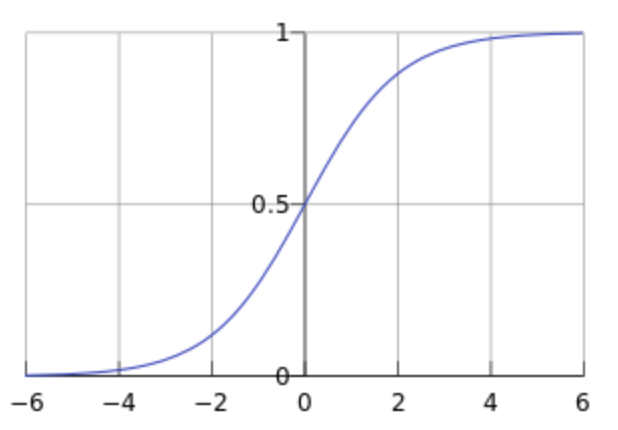
补充：Sigmoid函数求导结果：$\frac{dg(z)}{dz}=g(z)(1-g(z))$

假设函数

逻辑回归的假设函数：

$$h_{\theta}(x)=g\left(\theta^{T} x\right), g(z)=\frac{1}{1+e^{-z}}$$

故，得到最终假设函数为：

$$h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T} x}}$$

其中，$x$是输入样本，$\theta$是待求参数。

故，逻辑回归模型所做的假设（也就是 对假设函数输出值的解释）是，在给定$x$和$\theta$下，分类结果$y=1$的概率，即：$P(y=1 \mid x ; \theta)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta^{T} x}}$。

当构造出这个假设函数后，那么就需要通过学习来确定合适的$\theta$来拟合训练数据：构造损失函数，使其最小。

决策边界（Decision Boundary）

• 在N维空间，将不同类别样本分开的平面或曲面，也就是一个方程
• 是假设函数的属性，由假设函数的参数$\theta$决定，而不是由数据集的特征决定

下图的决策边界即为：$-3+x_1+x_2=0$

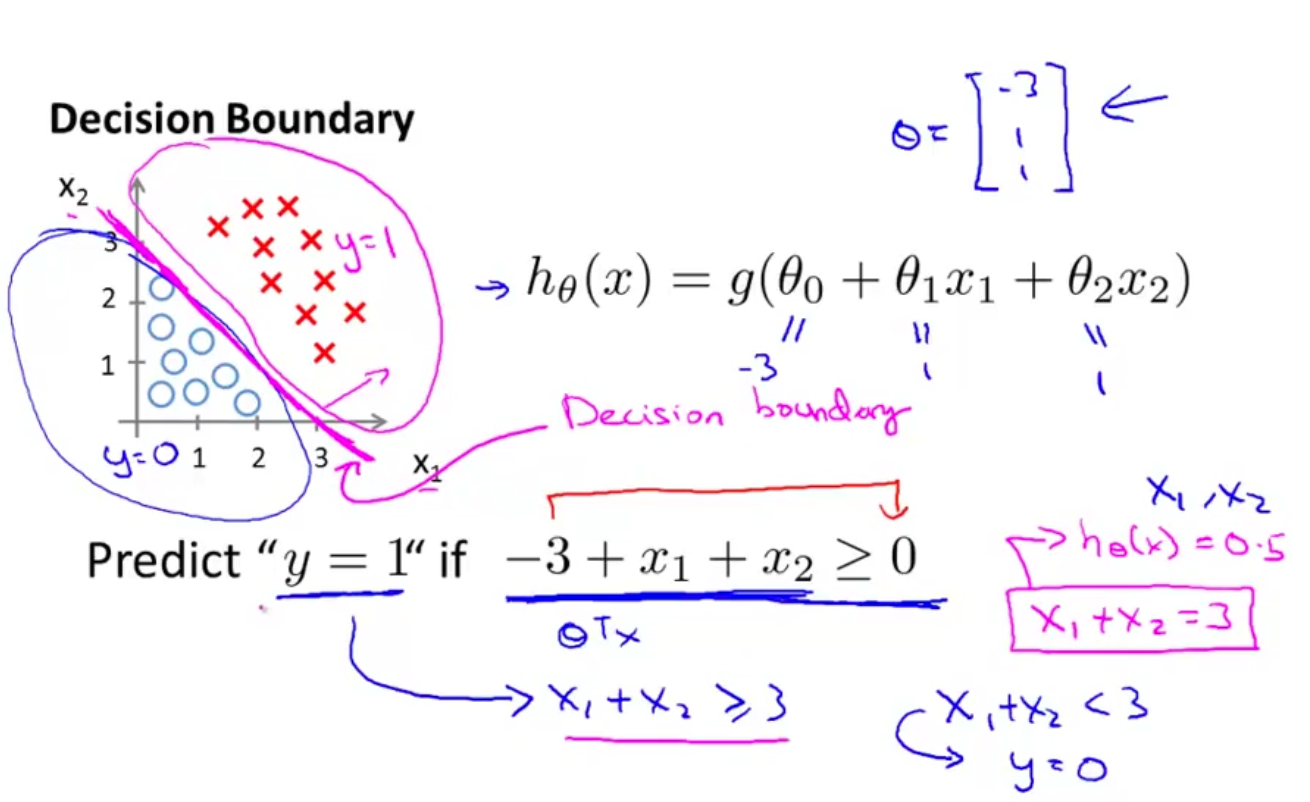
✔总结：

• 假设函数：$h=g(z)$用于计算样本属于某类别的可能性
• 决策函数：$y$* $=1,if P(y=1\vert x)\gt 0.5$用于计算样本的类别
• 决策边界，$\theta^{T}x=0$ 用于标识分类边界

损失函数（Cost Function）

训练集：$ \left\{\left(x^{(1)}, y^{(1)}\right),\left(x^{(2)}, y^{(2)}\right), \cdots,\left(x^{(m)}, y^{(m)}\right)\right\}$

对于每个训练样本：

$$x \in\left[\begin{array}{l} x_{0} \\ x_{1} \\ \cdots \\ x_{n} \end{array}\right] \quad x_{0}=1, y \in\{0,1\}$$

逻辑回归的损失函数：